题目内容
4.点A(x1,y1),B(x2,y2),C(x3,y3)都在反比例函数y=$\frac{-{k}^{2}-1}{x}$的图象上,若x1<x2<0<x3,则y1,y2,y3的大小关系是( )| A. | y3<y1<y2 | B. | y1<y2<y3 | C. | y3<y2<y1 | D. | y2<y1<y3 |
分析 先根据反比例函数的解析式判断出函数图象所在的象限,再根据x1<x2<0<x3即可得出结论.
解答 解:∵反比例函数y=$\frac{-{k}^{2}-1}{x}$中,k=-k2-1<0,
∴函数图象的两个分支分别位于二、四象限,且在每一象限内,y随x的增大而增大.
∵x1<x2<0,
∴A、B两点在第二象限,C点在第三象限,
∴y2>y1>y3.
故选A.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
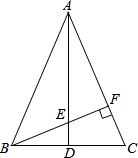 如图,△ABC中,AD⊥BC,BE的延长线交AC于点F,且BF⊥AC于F,∠BAC=45°,试证明:△AEF≌△BCF.
如图,△ABC中,AD⊥BC,BE的延长线交AC于点F,且BF⊥AC于F,∠BAC=45°,试证明:△AEF≌△BCF.