题目内容
20.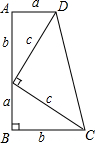 勾股定理的证明方法很多,下面是美国第20任总统加菲尔德用此图证明了勾股定理,你也来用此图试一试,验证:a2+b2=c2.
勾股定理的证明方法很多,下面是美国第20任总统加菲尔德用此图证明了勾股定理,你也来用此图试一试,验证:a2+b2=c2.
分析 因为梯形的上底为a,下底为b,高为(a+b),则它的面积可表示为$\frac{1}{2}$(a+b)•(a+b);此梯形的面积还可以看成是三个直角三角形的面积和,即$\frac{1}{2}$(ab×2+c2);则$\frac{1}{2}$(a+b)(a+b)=$\frac{1}{2}$(ab×2+c2),进而得出即可.
解答 证明:由题意可知梯形面积为$\frac{1}{2}$(a+b)(a+b);
此梯形的面积还可以看成是三个直角三角形的面积和,即$\frac{1}{2}$(ab×2+c2).
因此$\frac{1}{2}$(a+b)(a+b)=$\frac{1}{2}$(ab×2+c2),
即a2+b2=c2.
点评 此题主要考查了勾股定理的证明,主要应用梯形的面积公式和三角形的面积公式得出是解题关键.

练习册系列答案
相关题目
8.在-(-2),|-1|,-|0|,-22,(-3)2,-(-4)3中,正数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12.函数y=$\sqrt{x-5}+\sqrt{x+5}$的自变量x的取值范围是( )
| A. | x>5 | B. | x>-5 | C. | -5<x<5 | D. | x≥5 |
 如图,已知一商场自动扶梯的长L为10米,该自动扶梯到达的高度h为6米,自动扶
如图,已知一商场自动扶梯的长L为10米,该自动扶梯到达的高度h为6米,自动扶