题目内容
已知∠A、∠B、∠C是三角形ABC的三个内角,并且∠A-∠B=28°,∠B-∠C=34°,请问△ABC是否为直角三角形?为什么?
考点:三角形内角和定理
专题:
分析:首先设出∠A、∠B、∠C的度数分别为α、β、γ,列出关于α、β、γ的方程组,解方程组,即可解决问题.
解答:解:△ABC是直角三角形;理由如下:
设∠A、∠B、∠C的度数分别为α、β、γ;
则α+β+γ=180°①,α-β=28°②,β-γ=34°③;
由①+②得:2α+γ=208°④,
由②+③得:α-γ=62°⑤,
由④+⑤得:3α=270°,
∴α=90°,
∴△ABC是直角三角形.
设∠A、∠B、∠C的度数分别为α、β、γ;
则α+β+γ=180°①,α-β=28°②,β-γ=34°③;
由①+②得:2α+γ=208°④,
由②+③得:α-γ=62°⑤,
由④+⑤得:3α=270°,
∴α=90°,
∴△ABC是直角三角形.
点评:该题主要考查了三角形的内角和定理及其应用问题;解题的关键是灵活运用三角形的内角和定理来分析、判断、推理或解答.

练习册系列答案
相关题目
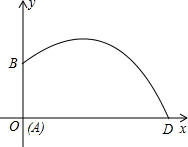 如图,某喷灌设备的喷头B高出地面1.2m,如果喷出的抛物线形水流的水平距离x(m)与高度y(m)之间关系为y=a(x-4)2+2,求水流落地点D与喷头底部A的距离(精确到0.1m)
如图,某喷灌设备的喷头B高出地面1.2m,如果喷出的抛物线形水流的水平距离x(m)与高度y(m)之间关系为y=a(x-4)2+2,求水流落地点D与喷头底部A的距离(精确到0.1m) 如图,已知∠AOB=60°,点P在边OA上,OP=12,点M、N在边OB上,PM=PN,MN=2,求△POM的面积.
如图,已知∠AOB=60°,点P在边OA上,OP=12,点M、N在边OB上,PM=PN,MN=2,求△POM的面积. 如图,在△ABC中,D、E、F分别是AB、AC、BC上的点,且DE∥BC,EF∥AB,求证:∠ADE=∠EFC.
如图,在△ABC中,D、E、F分别是AB、AC、BC上的点,且DE∥BC,EF∥AB,求证:∠ADE=∠EFC.