题目内容
18. 如图,△ABC中,AB=AC,∠A=36°,DE垂直平分AB交AC于D,交AB于E,下列论述错误的是( )
如图,△ABC中,AB=AC,∠A=36°,DE垂直平分AB交AC于D,交AB于E,下列论述错误的是( )| A. | BD平分∠ABC | B. | D是AC的中点 | ||
| C. | AD=BD=BC | D. | △BDC的周长等于AB+BC |
分析 由AB=AC,∠A=36°可求出两底角的大小,由根据线段垂直平分线的性质得∠A=∠ABD=36°,AD=BD等很多结论,利用这些结论对各选项进行逐一证明即可.
解答 解:A、∵△ABC中,AB=AC,∠A=36°,AB的中垂线DE交AC与D,交AB于E,
∴∠ABC=∠ACB=$\frac{1}{2}$(180°-∠A)=$\frac{1}{2}$(180°-36°)=72°
AD=BD,即∠A=∠ABD=36°
∴∠DBC=∠ABC-∠ABD=72°-36°=36°,故A正确;
B、条件不足,不能证明,故不对;
C、∵∠DBC=36°,∠C=72°
∴∠BDC=180°-72°-36°=72°,∠C=∠BDC
∵AD=BD
∴AD=BD=BC故C正确;
D、∵AD=BD
∴△BDC的周长等于AB+BC
故D正确;
故选B.
点评 本题考查了线段垂直平分线的性质,三角形内角与外角的关系,及等腰三角形的性质;尽量多的得出结论,对各选项逐一验证是正确解答本题的关键.

练习册系列答案
相关题目
11. 已知函数y=kx+b的图象如图所示,则一元二次方程x2+x+k-1=0根的情况是( )
已知函数y=kx+b的图象如图所示,则一元二次方程x2+x+k-1=0根的情况是( )
 已知函数y=kx+b的图象如图所示,则一元二次方程x2+x+k-1=0根的情况是( )
已知函数y=kx+b的图象如图所示,则一元二次方程x2+x+k-1=0根的情况是( )| A. | 没有实数根 | B. | 有两个相等的实数根 | ||
| C. | 有两个不相等的实数根 | D. | 不确定 |
6.下列算式能用平方差公式计算的是( )
| A. | (2a+b)(2b-a) | B. | (a+1)(-a-1) | C. | (3x-y)(-3x+y) | D. | (-m-n)(-m+n) |
13.下列运算正确的是( )
| A. | -2x2y•3xy2=-6x2y2 | B. | (x-2y)2=x2-4y2 | ||
| C. | (-4x2y2)2=16x4y9 | D. | 9x3y2÷3x2y=3xy |
1.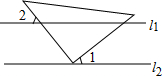 如图,直线l1∥l2,直角三角形ABC的直角顶点C在直线l2上,若∠1=30°,则∠2的度数为( )
如图,直线l1∥l2,直角三角形ABC的直角顶点C在直线l2上,若∠1=30°,则∠2的度数为( )
 如图,直线l1∥l2,直角三角形ABC的直角顶点C在直线l2上,若∠1=30°,则∠2的度数为( )
如图,直线l1∥l2,直角三角形ABC的直角顶点C在直线l2上,若∠1=30°,则∠2的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
8.下列命题中,真命题是( )
| A. | 对角互补的平行四边形是矩形 | |
| B. | 对角线相等的四边形是矩形 | |
| C. | 对角线互相垂直的四边形是菱形 | |
| D. | 对角线互相垂直平分的四边形是正方形 |
5.Rt△ABC中,∠B=90°,AB=3,BC=4,BD是AC边上中线,BH是AC边上高,则BD与BH的值分别是( )
| A. | 5,2.4 | B. | 2.5,$\sqrt{7}$ | C. | 2.5,2.5 | D. | 2.5,2.4 |
5.计算(-2)99+(-2)100的结果为( )
| A. | 299 | B. | 2100 | C. | -299 | D. | -2 |
 的步骤如下:
的步骤如下: ;
; ;
; ;
; .
. 不是原方程的解.请你检查一下,并予以改正.
不是原方程的解.请你检查一下,并予以改正.