题目内容
20.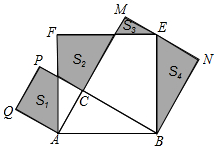 如图,Rt△ABC中,∠C=90°,AC=3,BC=4.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN,四块阴影部分的面积分别为S1、S2、S3、S4.则S1-S2+S3+S4等于( )
如图,Rt△ABC中,∠C=90°,AC=3,BC=4.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BCMN,四块阴影部分的面积分别为S1、S2、S3、S4.则S1-S2+S3+S4等于( )| A. | 4 | B. | 6 | C. | 8 | D. | 12 |
分析 过F作AM的垂线交AM于D,通过证明S2=SRt△ABC;S3=SRt△AQF=SRt△ABC;S4=SRt△ABC,进而即可求解.
解答  解:过F作AM的垂线交AM于D,
解:过F作AM的垂线交AM于D,
可证明Rt△ADF≌Rt△ABC,Rt△DFK≌Rt△CAT,
所以S2=SRt△ABC.
由Rt△DFK≌Rt△CAT可进一步证得:Rt△FPT≌Rt△EMK,
∴S3=S△FPT,
又可证得Rt△AQF≌Rt△ACB,
∴S1+S3=SRt△AQF=SRt△ABC.
易证Rt△ABC≌Rt△EBN,
∴S4=SRt△ABC,
∴S1-S2+S3+S4
=(S1+S3)-S2+S4
=SRt△ABC-SRt△ABC+SRt△ABC
=6-6+6
=6,
故选B.
点评 本题考查勾股定理的知识,有一定难度,解题关键是将勾股定理和正方形的面积公式进行灵活的结合和应用.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
10.已知P(a,b),其中a>0,b<0,那么点P关于x轴的对称点Q在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8.已知等腰三角形一边长为2,一边的长为4,则这个等腰三角形的周长为( )
| A. | 8 | B. | 9 | C. | 10 | D. | 8或10 |
9.下列等式从左到右的变形是因式分解的是( )
| A. | 6x2y2=xy•6xy | B. | 2x2-8x-5=2x(x-4)-5 | ||
| C. | x2+3x-4=(x-1)(x+4) | D. | x2+1=x(x+$\frac{1}{x}$) |
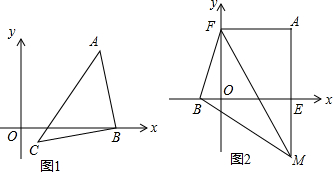
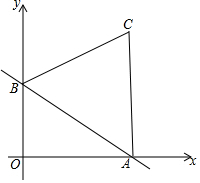 如图.直线y=-$\frac{\sqrt{3}}{3}$x+1和x、y轴分别交于点A、B,∠BAO=30°,以线段AB为边在第一象限内作等边三角形ABC.如果在第一象限内有一点P(m,1),且△ABP的面积与△ABC的面积相等,求m的值.
如图.直线y=-$\frac{\sqrt{3}}{3}$x+1和x、y轴分别交于点A、B,∠BAO=30°,以线段AB为边在第一象限内作等边三角形ABC.如果在第一象限内有一点P(m,1),且△ABP的面积与△ABC的面积相等,求m的值.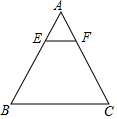 如图,在△ABC中,EF∥BC,$\frac{AE}{EB}$=$\frac{1}{2}$,EF=3,则BC的值为9.
如图,在△ABC中,EF∥BC,$\frac{AE}{EB}$=$\frac{1}{2}$,EF=3,则BC的值为9.