题目内容
在△ABC中,AB=AC=5,cos∠ABC=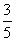 ,将△ABC绕点C顺时针旋转,得到△A1B1C。(1)如图①,当点B1在线段BA延长线上时。①求证:BB1∥CA1;②求△AB1C的面积;
,将△ABC绕点C顺时针旋转,得到△A1B1C。(1)如图①,当点B1在线段BA延长线上时。①求证:BB1∥CA1;②求△AB1C的面积;
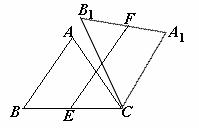
(2)如图②,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1,求线段EF1长度的最大值与最小值的差。
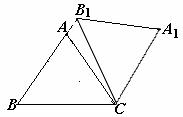
解:(1)①证明:∵AB=AC,B1C=BC ∴∠1=∠B,∠B=∠ACB,∵∠2=∠ACB(旋转角相等),∴∠1=∠2 ∴BB1∥CA1
②过A作AF⊥BC于F,过C作CE⊥AB于E
 ∵AB=AC,AF⊥BC
∵AB=AC,AF⊥BC
∴BF=CF
∵cos∠ABC=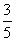 ,AB=5,
,AB=5,
∴BF=3
∴BC=6
∴B1C=BC=6
∵CE⊥AB
∴BE=B1E=
∴BB1= ,CE=
,CE=
∴AB1= ,
,
∴△AB1C的面积为:
(2)如图过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,EF1有最小值。
此时在Rt△BFC中,CF= ,
,
∴CF1= ,
,
∴EF1的最小值为 ;
;
如图,以C为圆心BC为半径画圆交BC的延长线于F1,EF1有最大值。
此时EF1=EC+CF1=3+6=9
∴线段EF1的最大值与最小值的差为 。
。


练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
 向排列,若在平面直角坐标系内, B、D 两点对应的坐
向排列,若在平面直角坐标系内, B、D 两点对应的坐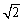 ,
, )
) 平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函
平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函 的图象上,过点A的直线y=x+b交x轴于点B.
的图象上,过点A的直线y=x+b交x轴于点B.
 =
=
 BC
BC
 与甲盒数量
与甲盒数量 之间的函数关系式,并求出最少需要多少米材料。
之间的函数关系式,并求出最少需要多少米材料。