Question

【题目】如图，在矩形中，，，将点绕点逆时针旋转，点的对应点为.的平分线交于，且.若点落在矩形的边上，则的值为______.

Answer 1

【答案】或

【解析】

分两种情况：①点B′落在AD边上，根据矩形与折叠的性质易得AB＝BE，即可求出a的值；②点B′落在CD边上，证明△ADB′∽△B′CE，根据相似三角形对应边成比例即可求出a的值．

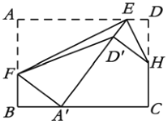
解：分两种情况：①当点B′落在AD边上时，如图1．
∵四边形ABCD是矩形，
∴∠BAD＝∠B＝90°，
∵将△ABE沿AE折叠，点B的对应点B′落在AD边上，
∴∠BAE＝∠B′AE＝∠BAD＝45°，
∴AB＝BE，
∴a＝1，
∴a＝；

②当点B′落在CD边上时，如图2．
∵四边形ABCD是矩形，
∴∠BAD＝∠B＝∠C＝∠D＝90°，AD＝BC＝a．
∵将△ABE沿AE折叠，点B的对应点B′落在CD边上，
∴∠B＝∠AB′E＝90°，AB＝AB′＝1，EB＝EB′＝a，
∴DB′＝＝，EC＝BCBE＝aa＝a．
∵∠B′AD＝∠EB′C＝90°∠AB′D，
∠D＝∠C＝90°，
∴△ADB′∽△B′CE，
∴ ，即，
解得a1＝，a2＝（舍去）．
综上，所求a的值为或．
故答案为或．