题目内容
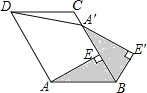
【题目】如图,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得到
得到![]() .
.
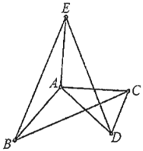
(1)观察猜想
小明发现,将![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() ,如图1,他发现
,如图1,他发现![]() 的面积
的面积![]() 与
与![]() 的面积
的面积![]() 之间有一定的数量关系,请直接写出这个关系:______;
之间有一定的数量关系,请直接写出这个关系:______;
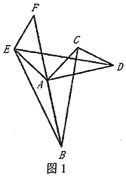
(2)类比探究
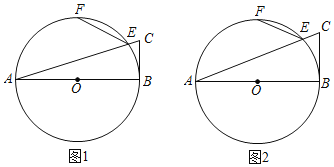
如图2,![]() 是
是![]() 的中点,请写出
的中点,请写出![]() 与
与![]() 之间的数量关系和位置关系,并说明理由;
之间的数量关系和位置关系,并说明理由;
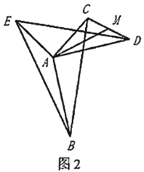
(3)解决问题
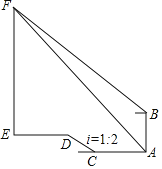
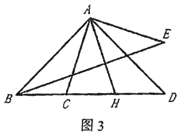
如图3,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 在线段
在线段![]() 上,
上,![]() 交
交![]() 于
于![]() ,若
,若![]() ,
,![]() ,请直接写出
,请直接写出![]() 的长.
的长.
【答案】(1)![]() ;(2)BE=2AM,
;(2)BE=2AM,![]() ,理由见解析;(3)
,理由见解析;(3)![]()
【解析】
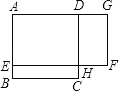
(1)结论:S1=S2.如图1中,作EH⊥BA交BA的延长线于H,CM⊥AD于M,利用三角形的面积公式证明即可;
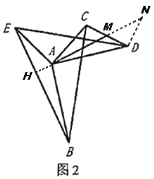
(2)如图2中,延长![]() 至点
至点![]() 使得
使得![]() ,连接
,连接![]() ,易证
,易证![]() ,求出
,求出![]() ,然后证明
,然后证明![]() ,得到
,得到![]() ,
,![]() ,延长
,延长![]() 交
交![]() 于点
于点![]() ,求出
,求出![]() 即可;
即可;
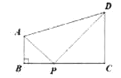
(3)作DT∥AC交AH的延长线于T.连接DE.证明△BAC≌△DAE(SAS),推出∠ADE=∠ABC=45°,BC=DE=2,推出∠BDE=∠BDA+∠ADE=90°,推出![]() ,再证明AH=
,再证明AH=![]() BE即可解决问题.
BE即可解决问题.
解:(1)结论:S1=S2.
理由:如图1中,作EH⊥BA交BA的延长线于H,CM⊥AD于M.
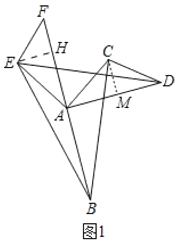
由题意CA=AE,AD=AB,∠CAE=∠DAF=90°,
∴∠EAH=∠CAM,
∴sin∠CAM=sin∠EAH,
∵S1=![]() ADCM=
ADCM=![]() ADACsin∠CAM,S2=
ADACsin∠CAM,S2=![]() ABEH=
ABEH=![]() ABAEsin∠EAH,
ABAEsin∠EAH,
∴S1=S2.
故答案为S1=S2;
(2)结论:BE=2AM,![]() ;
;
理由:延长![]() 至点
至点![]() 使得
使得![]() ,连接
,连接![]() ,
,
易证![]() ,
,
∴![]() 且
且![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
延长![]() 交
交![]() 于点
于点![]() ,
,
在![]() 中,
中,![]()
![]()
![]() ,
,
∴![]() ,
,
∴![]() ;
;
(3)作DT∥AC交AH的延长线于T,连接DE.
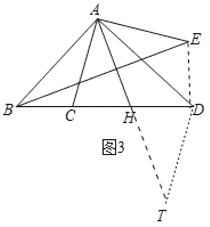
∵AB=AD,AC=AE,∠BAD=∠CAE=90°,
∴∠ABD=∠ADB=45°,∠BAC=∠DAE,
∴△BAC≌△DAE(SAS),
∴∠ADE=∠ABC=45°,BC=DE=2,
∴∠BDE=∠BDA+∠ADE=90°,
∴BE=![]() ,
,
∵∠BAD=∠CAE=90°,
∴∠CAD+∠BAE=180°,
∵AC∥DT,
∴∠CAD+∠ADT=180°,
∴∠BAE=∠ADT,
∵AH⊥BE,
∴∠DAT+∠BAT=90°,∠ABE+∠BAT=90°,
∴∠DAT=∠ABE,
∵AB=AD,
∴△ABE≌△DAT(ASA),
∴BE=AT,AE=DT,
∵AC=AE,
∴AC=DT,
∵∠CAH=∠T,∠AHC=∠DHT,
∴△AHC≌△THD(AAS),
∴AH=HT,
∴AH=![]() BE=
BE=![]() .
.

 全优点练单元计划系列答案
全优点练单元计划系列答案