题目内容
13.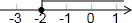 如图,数轴上表示的是某个函数自变量的取值范围,则这个函数解析式为( )
如图,数轴上表示的是某个函数自变量的取值范围,则这个函数解析式为( )| A. | y=x+2 | B. | y=x2+2 | C. | y=$\sqrt{x+2}$ | D. | y=$\frac{1}{x+2}$ |
分析 分别求出个解析式的取值范围,对应数轴,即可解答.
解答 解:A、y=x+2,x为任意实数,故错误;
B、y=x2+2,x为任意实数,故错误;
C、$y=\sqrt{x+2}$,x+2≥0,即x≥-2,故正确;
D、y=$\frac{1}{x+2}$,x+2≠0,即x≠-2,故错误;
故选:C.
点评 本题考查了函数自变量的取值范围,解决本题的关键是函数自变量的范围一般从三个方面考虑:
(1)当函数表达式是整式时,自变量可取全体实数;
(2)当函数表达式是分式时,考虑分式的分母不能为0;
(3)当函数表达式是二次根式时,被开方数非负.

练习册系列答案
相关题目
3.已知四边形ABCD,下列说法正确的是( )
| A. | 当AD=BC,AB∥DC时,四边形ABCD是平行四边形 | |
| B. | 当AD=BC,AB=DC时,四边形ABCD是平行四边形 | |
| C. | 当AC=BD,AC平分BD时,四边形ABCD是矩形 | |
| D. | 当AC=BD,AC⊥BD时,四边形ABCD是正方形 |
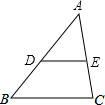 如图,在△ABC中,D、E分别是AB、AC边的中点.求证:DE$\stackrel{∥}{=}$$\frac{1}{2}$BC.
如图,在△ABC中,D、E分别是AB、AC边的中点.求证:DE$\stackrel{∥}{=}$$\frac{1}{2}$BC.
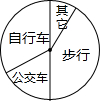 某学校要了解学生上学交通情况,选取九年级全体学生进行调查,根据调查结果,画出扇形统计图(如图),图中“公交车”对应的扇形圆心角为60°,“自行车”对应的扇形圆心角为120°,已知九年级乘公交车上学的人数为50人.
某学校要了解学生上学交通情况,选取九年级全体学生进行调查,根据调查结果,画出扇形统计图(如图),图中“公交车”对应的扇形圆心角为60°,“自行车”对应的扇形圆心角为120°,已知九年级乘公交车上学的人数为50人.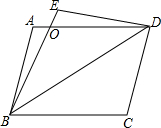 在平行四边形ABCD中,将△BCD沿BD翻折,使点C落在点E处,BE和AD相交于点O,求证:OA=OE.
在平行四边形ABCD中,将△BCD沿BD翻折,使点C落在点E处,BE和AD相交于点O,求证:OA=OE. 以正方形ABCD两条对角线的交点O为坐标原点,建立如图所示的平面直角坐标系,双曲线y=$\frac{3}{x}$经过点D,则正方形ABCD的面积是( )
以正方形ABCD两条对角线的交点O为坐标原点,建立如图所示的平面直角坐标系,双曲线y=$\frac{3}{x}$经过点D,则正方形ABCD的面积是( )