题目内容
10.某商店经销一种销售成本为每千克40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500kg;销售单价每涨1元,月销售量就减少10kg.针对这种水产品的销售情况,请解答以下问题:(1)设销售单价为每千克x元,月销售利润为y元,求y与x的函数关系式;
(2)在使顾客获得实惠的条件下,要使月销售利润达到8000元,销售单价应定为多少?
(3)在月销售成本不超过10000元的情况下,销售单价定为多少时,月销售利润达到最大?
分析 (1)根据题意可以列出y关于x的函数关系式;
(2)令y=8000代入(1)中的函数关系式,可以求得销售单价,还要注意要使顾客获得实惠,可知利润不变的情况下,降价越多,顾客获得的实惠越多;
(3)将(1)中函数关系式化为顶点式,再根据月销售成本不超过10000元,可以求得销售单价定为多少时,月销售利润达到最大.
解答 解:(1)由题意可得,
y=(x-40)[500-(x-50)×10]=-10x2+1400x-40000,
即y与x的函数关系式是:y=-10x2+1400x-40000;
(2)将y=8000代入y=-10x2+1400x-40000,得
-10x2+1400x-40000=8000,
解得,x=60或x=80,
∵要使顾客获得实惠,
∴定价为每千克80元,
即在使顾客获得实惠的条件下,要使月销售利润达到8000元,销售单价应定为每千克80元;
(3)∵y=-10x2+1400x-40000=-10(x-70)2+9000,
又∵40×[500-(x-50)×10]≤10000,
解得,x≥75,
∴当x=75时,月销售利润最大,
即在月销售成本不超过10000元的情况下,销售单价定为每千克75元时,月销售利润达到最大.
点评 本题考查二次函数的应用,解题的关键是明确题意,找出所求问题需要的条件,根据题意可以列出相应的函数关系式,可以发现题目中的隐含条件,如要使顾客获得实惠.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
1.下列说法正确的是( )
| A. | 调查重庆市空气质量情况应该采用普查的方式 | |
| B. | A组数据方差$S_A^2=0.03$,B组数据方差$S_B^2=0.2$,则B组数据比A组数据稳定 | |
| C. | 重庆八中明年开运动会一定不会下雨 | |
| D. | 2,3,6,9,5这组数据的中位数是5 |
18.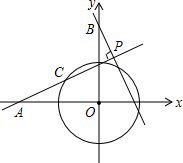 如图,在平面直角坐标系xOy中,A(-2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为( )
如图,在平面直角坐标系xOy中,A(-2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为( )
 如图,在平面直角坐标系xOy中,A(-2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为( )
如图,在平面直角坐标系xOy中,A(-2,0),B(0,2),⊙O的半径为1,点C为⊙O上一动点,过点B作BP⊥直线AC,垂足为点P,则P点纵坐标的最大值为( )| A. | $2\sqrt{2}$ | B. | $\frac{{\sqrt{3}+1}}{2}$ | C. | 2 | D. | $\frac{3}{2}$ |
5. 为响应我市“中国梦”•“株洲梦”主题教育活动,某中学在全校学生中开展了以“中国梦•我的梦”为主题的征文比赛,评选出一、二、三等奖和优秀奖.孔明同学根据获奖结果,绘制成如图所示的统计表和数学统计图.
为响应我市“中国梦”•“株洲梦”主题教育活动,某中学在全校学生中开展了以“中国梦•我的梦”为主题的征文比赛,评选出一、二、三等奖和优秀奖.孔明同学根据获奖结果,绘制成如图所示的统计表和数学统计图.
请你根据图表提供的信息,解答下列问题:
(1)完成表格和扇形统计图:a=5,b=20,n=144.
(2)学校决定在获得一等奖的作者中,随机推荐两名作者代表学校参加市级比赛,其中王梦、李刚都获得一等奖,请用画树状图或列表的方法,求恰好选中这二人的概率.
 为响应我市“中国梦”•“株洲梦”主题教育活动,某中学在全校学生中开展了以“中国梦•我的梦”为主题的征文比赛,评选出一、二、三等奖和优秀奖.孔明同学根据获奖结果,绘制成如图所示的统计表和数学统计图.
为响应我市“中国梦”•“株洲梦”主题教育活动,某中学在全校学生中开展了以“中国梦•我的梦”为主题的征文比赛,评选出一、二、三等奖和优秀奖.孔明同学根据获奖结果,绘制成如图所示的统计表和数学统计图.| 等级 | 频数 | 频率 |
| 一等奖 | a | 0.1 |
| 二等奖 | 10 | 0.2 |
| 三等奖 | b | 0.4 |
| 优秀奖 | 15 | 0.3 |
(1)完成表格和扇形统计图:a=5,b=20,n=144.
(2)学校决定在获得一等奖的作者中,随机推荐两名作者代表学校参加市级比赛,其中王梦、李刚都获得一等奖,请用画树状图或列表的方法,求恰好选中这二人的概率.
19.多项式x2-4x-12可以因式分解成( )
| A. | x(x-4)-12 | B. | (x-2)(x+6) | C. | (x+2)(x-6) | D. | (x+3)(x-4) |