Question

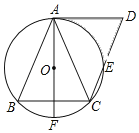
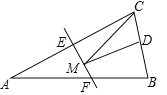
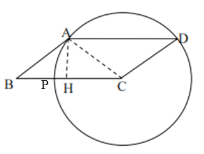
【题目】如图，已知在平行四边形ABCD中，AB＝10，BC＝16，cosB＝，点P是边BC上的动点，以CP为半径的圆C与边AD交于点E、F（点F在点E的右侧），射线CE与射线BA交于点G．

（1）当圆C经过点A时，求CP的长

（2）联结AP，当AP//CG时，求弦EF的长

（3）当△AGE是等腰三角形时，求圆C的半径长．

Answer 1

【答案】（1）10；（2）；（3）

【解析】

（1）当点A在⊙C上时，点E和点A重合，过点A作AH⊥BC于H，根据，求出BH的长度，得出AH垂直平分BC，由垂直平分线的性质得到AB=AC，从而得到CP=AC即可；
（2）首先得出四边形APCE是菱形，进而得出CN的长，进而利用锐角三角函数关系得出CP，再由勾股定理及垂径定理求出EF的长；
（3）∠GAE≠∠BGC，只能∠AGE＝∠AEG，利用AD∥BC，得出△GAE∽△GBC，列出相似比解出AE=6，从而得出EN的值，再由勾股定理即可求出CE的值．

解：（1）过点A作AH⊥BC，垂足为H，联结AC．

在Rt△AHB中，∠AHB＝90°，

∵AB＝10，

∴BH＝8，AH=

∵BC＝16，

∴AH垂直平分BC，

∴AB＝AC＝10，

∵圆C经过点A，

∴CP＝AC＝10，

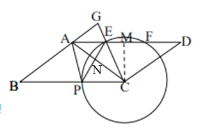
（2）过点C作CM⊥AD，垂足为M，

∵四边形ABCD是平行四边形，

AD∥BC，

若AP//CG，

则四边形APCE为平行四边形，

∵CE=CP，

∴平行四边形APCE是菱形，

连接AC，PE交于点N，则AC⊥PE，

∴AN=CN=，

由（1）可知AC=AB=10，CM=AH=6

∴AN=CN=5，∠ABC=∠ACB，

∴CP=CE=，

则EF=2EM=，

∴当AP∥CG时，弦EF的长为．

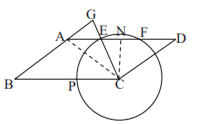
（3）∵，

∴∠B﹤45°，

又∵∠BCG﹤90°，

∴∠BGC﹥45°，

又∵∠AEG＝∠BCG≥∠ACB＝∠B，

∴当∠AEG＝∠B时，A、E、G重合，

只能∠AGE＝∠AEG，

∵AD∥BC，

∴△GAE∽△GBC

∴，即，解得

∴EN＝AN－AE＝2，

∴．

∴圆C的半径长为