题目内容
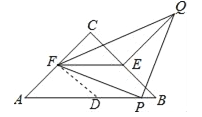
【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,点E、F分别是边BC、AC的中点,P是AB上一点,以PF为一直角边作等腰直角三角形PFQ,且∠FPQ=90°,若AB=10,PB=1,则QE的值为( )

A. 3 B. 3![]() C. 4 D. 4
C. 4 D. 4![]()
【答案】D
【解析】解:连结FD,D是AB的中点,如图.∵△ABC为等腰直角三角形,AB=10,PB=1,∴AC=BC=![]() ,∠A=45°.∵点D、E、F分别是△ABC三边的中点,AB=10,PB=1,∴AD=BD= 5,DP=DB﹣PB=5﹣1=4,EF、DF为△ABC的中位线,∴EF∥AB,EF=
,∠A=45°.∵点D、E、F分别是△ABC三边的中点,AB=10,PB=1,∴AD=BD= 5,DP=DB﹣PB=5﹣1=4,EF、DF为△ABC的中位线,∴EF∥AB,EF= ![]() AB=5,DF=
AB=5,DF= ![]() BC=
BC=![]() ,∠EFP=∠FPD,∴∠FDA=45°,
,∠EFP=∠FPD,∴∠FDA=45°,![]() =
=![]() =
=![]() ,∴∠DFP+∠DPF=45°.∵△PQF为等腰直角三角形,∴∠PFE+∠EFQ=45°,FP=PQ,∴∠DFP=∠EFQ.∵△PFQ是等腰直角三角形,∴
,∴∠DFP+∠DPF=45°.∵△PQF为等腰直角三角形,∴∠PFE+∠EFQ=45°,FP=PQ,∴∠DFP=∠EFQ.∵△PFQ是等腰直角三角形,∴![]() =
= ![]() ,∴
,∴![]() =
= ![]() ,∴△FDP∽△FEQ,∴
,∴△FDP∽△FEQ,∴![]() =
=![]() ,∴QE=
,∴QE= ![]() DP=
DP=![]() .故选D.
.故选D.

练习册系列答案
相关题目