题目内容
3．
如图，已知EF∥BD，∠1=∠2，∠C=48°，求∠ABC．
分析 首先由平行线的性质易得∠1=∠ABD，等量代换得∠2=∠ABD，利用平行线的判定定理可得AB∥CD，由平行线的性质，两直线平行，同旁内角互补可得∠ABC+∠C=180°，代入得出结论．
解答 解：∵EF∥BD，
∴∠1=∠ABD，
∵∠1=∠2，
∴∠2=∠ABD，
∴AB∥CD，
∴∠ABC+∠C=180°，
∵∠C=48°，
∴∠ABC=132°．
点评 本题主要考查了平行线的性质及判定定理，综合运用平行线的性质和判定定理，等量代换是解答此题的关键．
练习册系列答案
三新快车金牌周周练系列答案
相关题目
13．
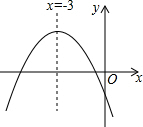二次函数y=ax2+bx+c的图象如图所示，已知A（-1，y），B（-4，y2）和C（-5，y3）都在此图象上，下列关系式正确的是（ ）
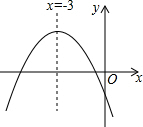二次函数y=ax2+bx+c的图象如图所示，已知A（-1，y），B（-4，y2）和C（-5，y3）都在此图象上，下列关系式正确的是（ ）| A． | y1＜y3＜y2 | B． | y1＞y2＞y3 | C． | y3＜y2=y1 | D． | y1=y3＜y2 |
14．不等式5x≤-10的解集在数轴上表示为（ ）
| A． |  | B． |  | C． |  | D． |  |
8．
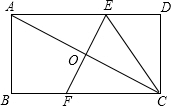如图，在矩形ABCD中，AB=2，BC=4，将矩形沿EF折叠，使点A与点C重合，连接CE，则CE长为（ ）
如图，在矩形ABCD中，AB=2，BC=4，将矩形沿EF折叠，使点A与点C重合，连接CE，则CE长为（ ）| A． | 3.5 | B． | 3 | C． | 2.8 | D． | 2.5 |
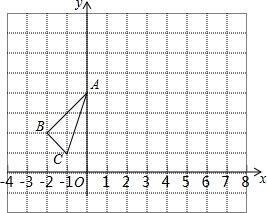△ABC在平面直角坐标系中的位置如图所示，点O为坐标原点：