题目内容
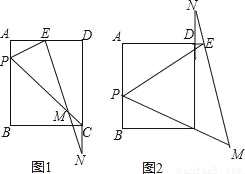
如图1,矩形ABCD中,P是AB边上的一点(不与A,B重合),PE平分∠APC交射线AD于E,过E作EM⊥PE交直线CP于M,交直线CD于N.
(1)求证:CM=CN;
(2)若AB:BC=4:3,
①当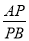 = 时,E恰好是AD的中点;
= 时,E恰好是AD的中点;
②如图2,当△PEM与△PBC相似时,求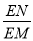 的值.
的值.
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
如图1,矩形ABCD中,P是AB边上的一点(不与A,B重合),PE平分∠APC交射线AD于E,过E作EM⊥PE交直线CP于M,交直线CD于N.
(1)求证:CM=CN;
(2)若AB:BC=4:3,
①当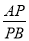 = 时,E恰好是AD的中点;
= 时,E恰好是AD的中点;
②如图2,当△PEM与△PBC相似时,求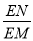 的值.
的值.

 阅读快车系列答案
阅读快车系列答案