��Ŀ����
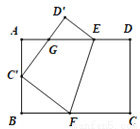
��ͼ��������ABCD��EF�۵���ʹ����Cǡ������AB�ߵ�C'������D���ڵ�D'����C'D'���߶�AE�ڵ�G.
��1����֤����BC'F�ס�AGC'��
��2����C'��AB���е㣬AB=6��BC=9����AG�ij�.
��ϰ��ϵ�д�
�����Ŀ
��Ŀ����
��ͼ��������ABCD��EF�۵���ʹ����Cǡ������AB�ߵ�C'������D���ڵ�D'����C'D'���߶�AE�ڵ�G.
��1����֤����BC'F�ס�AGC'��
��2����C'��AB���е㣬AB=6��BC=9����AG�ij�.
