题目内容
1.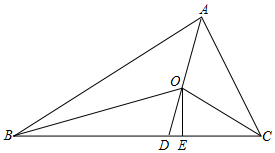 如图,△ABC中,∠ACB>∠ABC,点O是△ABC的内角平分线的交点,AO的延长线交BC于点D,OE⊥BC于点E
如图,△ABC中,∠ACB>∠ABC,点O是△ABC的内角平分线的交点,AO的延长线交BC于点D,OE⊥BC于点E(1)若∠BAC=90°
①求∠BOC的度数
②如果∠DOE=15°,求∠EOC的度数
(2)设∠OBC=α,∠OCB=β,求∠DOE(用α、β表示)
分析 (1)①由三角形的内角和得到∠ABC+∠ACB=90°,根据角平分线的性质得到∠OBC=$\frac{1}{2}$∠ABC,∠OCD=$\frac{1}{2}$∠ACB,于是得到∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=45°,即可得到结论;
②由O是△ABC的三内角平分线的交点,得到∠ABO=$\frac{1}{2}$∠ABC,∠BAO=$\frac{1}{2}$∠BAC,∠OCB=$\frac{1}{2}$∠ACB,根据三角形的内角和得到∠BAC+∠ABC=180°-∠ACB,推出∠BOD=∠BAO+∠ABO=$\frac{1}{2}$(∠BAC+∠ABC)=$\frac{1}{2}$(180°-∠ACB)=90°-$\frac{1}{2}$∠ACB,根据三角形的内角和和角平分线的性质得到∠EOC=90°-$\frac{1}{2}$∠ACB,即可得到结果;
(2)根据已知条件得到DOE=$\frac{1}{2}$(∠ACB-∠ABC),再根据角平分线的定义代入即可求解.
解答 解:(1)①∵∠BAC=90°,
∴∠ABC+∠ACB=90°,
∵BO平分∠ABC,OC平分∠ACB,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCD=$\frac{1}{2}$∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=45°,
∴∠BOC=180°-(∠OBC+∠OCB)=135°;
②∵O是△ABC的三内角平分线的交点,
∴∠ABO=$\frac{1}{2}$∠ABC,∠BAO=$\frac{1}{2}$∠BAC,∠OCB=$\frac{1}{2}$∠ACB,
∵∠BAC+∠ABC+∠ACB=180°,
∴∠BAC+∠ABC=180°-∠ACB,
∴∠BOD=∠BAO+∠ABO=$\frac{1}{2}$(∠BAC+∠ABC)=$\frac{1}{2}$(180°-∠ACB)=90°-$\frac{1}{2}$∠ACB,
∵∠OEC=90°,∠OCB=$\frac{1}{2}$∠ACB,
∴∠EOC=90°-$\frac{1}{2}$∠ACB,
∴∠BOD=∠EOC=$\frac{1}{2}$(135°-15°)=60°;
(2)∠DOE=$\frac{1}{2}$(∠ACB-∠ABC)=β-α.
点评 本题考查了三角形的内角和,角平分线的性质,熟练掌握三角形的内角和是解题的关键.

| A. | 对角相等 | B. | 对边相等 | C. | 邻角互补 | D. | 对角线相等 |
| A. | $\sqrt{0.5}$ | B. | $\sqrt{\frac{1}{5}}$ | C. | $\sqrt{50}$ | D. | $\sqrt{3{x}^{2}+1}$ |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 已知数a、b、c在数轴上的位置如图所示,化简:|a+b|-|c-b|+2|c-a|的结果是3a-c.
已知数a、b、c在数轴上的位置如图所示,化简:|a+b|-|c-b|+2|c-a|的结果是3a-c.
 如图,在平面直角坐标系中,已知点B(4,2),A(4,0).
如图,在平面直角坐标系中,已知点B(4,2),A(4,0).