题目内容
15.先化简,再求值:(1+$\frac{1}{x-1}$)÷$\frac{1}{{x}^{2}-1}$-(x-2),然后从$\sqrt{2}$,1,-1中选取一个你认为合适的数作为x的值代入求值.
分析 根据分式的除法和加减法可以化简题目中的式子,然后选取一个使得原分式有意义的x的值代入即可解答本题.
解答 解:(1+$\frac{1}{x-1}$)÷$\frac{1}{{x}^{2}-1}$-(x-2)
=$\frac{x-1+1}{x-1}•(x+1)(x-1)-(x-2)$
=x(x+1)-x+2
=x2+x-x+2
=x2+2,
当x=$\sqrt{2}$时,原式=$(\sqrt{2})^{2}+2$=2+2=4.
点评 本题考查分式的化简求值,解答本题的关键是明确分式化简求值的方法.

练习册系列答案
相关题目
10.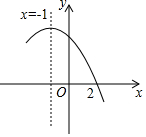 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,下列结论:①$\frac{a}{c}$<0;②a-b+c=-9a;③若(-3,y1),($\frac{3}{2}$,y2)是抛物线上两点,则y1>y2;④将抛物线沿x轴向右平移一个单位后得到的新抛物线的表达式为y=a(x2-9).其中正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,下列结论:①$\frac{a}{c}$<0;②a-b+c=-9a;③若(-3,y1),($\frac{3}{2}$,y2)是抛物线上两点,则y1>y2;④将抛物线沿x轴向右平移一个单位后得到的新抛物线的表达式为y=a(x2-9).其中正确的是( )
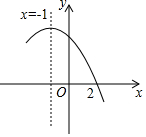 如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,下列结论:①$\frac{a}{c}$<0;②a-b+c=-9a;③若(-3,y1),($\frac{3}{2}$,y2)是抛物线上两点,则y1>y2;④将抛物线沿x轴向右平移一个单位后得到的新抛物线的表达式为y=a(x2-9).其中正确的是( )
如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,x=-1是对称轴,下列结论:①$\frac{a}{c}$<0;②a-b+c=-9a;③若(-3,y1),($\frac{3}{2}$,y2)是抛物线上两点,则y1>y2;④将抛物线沿x轴向右平移一个单位后得到的新抛物线的表达式为y=a(x2-9).其中正确的是( )| A. | ①②③ | B. | ①③④ | C. | ①②④ | D. | ①②③④ |
20. 如图,BO平分∠ABC,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=10,则△AMN的周长为( )
如图,BO平分∠ABC,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=10,则△AMN的周长为( )
 如图,BO平分∠ABC,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=10,则△AMN的周长为( )
如图,BO平分∠ABC,CO平分∠ACB,且MN∥BC,设AB=12,BC=24,AC=10,则△AMN的周长为( )| A. | 22 | B. | 36 | C. | 46 | D. | 34 |
16.一个布袋中装有22个质地相同的红、黑、黄三种颜色的小球,其中红色球有4个,黑色球有12个,从布袋中任意取出一个球,那么取到黄色球的可能性为( )
| A. | $\frac{2}{11}$ | B. | $\frac{3}{11}$ | C. | $\frac{5}{11}$ | D. | $\frac{6}{11}$ |
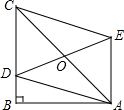 如图,在Rt△ABC中,∠B=90°,AB=10,BC>AB,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是10.
如图,在Rt△ABC中,∠B=90°,AB=10,BC>AB,点D在BC上,以AC为对角线的所有平行四边形ADCE中,DE的最小值是10.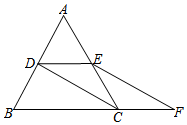 如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连结CD和EF.
如图,等边△ABC的边长是2,D、E分别为AB、AC的中点,延长BC至点F,使CF=$\frac{1}{2}$BC,连结CD和EF.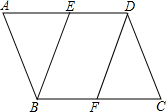 如图,在?ABCD中,点E、F分别在AD,BC上,且AE=CF,连接BE、DF
如图,在?ABCD中,点E、F分别在AD,BC上,且AE=CF,连接BE、DF