Question

6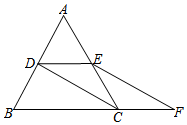．如图，等边△ABC的边长是2，D、E分别为AB、AC的中点，延长BC至点F，使CF=$\frac{1}{2}$BC，连结CD和EF．
（1）求证：四边形CDEF是平行四边形；
（2）求四边形BDEF的周长．

Answer 1

分析 （1）直接利用三角形中位线定理得出DE∥BC，再利用平行四边形的判定方法得出答案；
（2）利用等边三角形的性质结合平行四边形的性质得出DC=EF，进而求出四边形BDEF的周长．

解答 （1）证明：∵D、E分别是AB，AC中点，
∴DE∥BC，DE=$\frac{1}{2}$BC，
∵CF=$\frac{1}{2}$BC，
∴DE=CF，
∴四边形CDEF是平行四边形，

（2）解：∵四边形DEFC是平行四边形，
∴DC=EF，
∵D为AB的中点，等边△ABC的边长是2，
∴AD=BD=1，CD⊥AB，BC=2，
∴DC=EF=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$，
∴四边形BDEF的周长是1+1+2+1+$\sqrt{3}$=5+$\sqrt{3}$．

点评 此题主要考查了等边三角形的性质以及平行四边形的判定与性质、三角形中位线定理等知识，正确掌握平行四边形的性质是解题关键．