题目内容
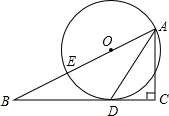 如图,已知点E在△ABC的边AB上,∠C=90°,∠BAC的平分线交BC于点D,且D在以AE为直径的⊙O上.
如图,已知点E在△ABC的边AB上,∠C=90°,∠BAC的平分线交BC于点D,且D在以AE为直径的⊙O上.(1)证明:BC是⊙O的切线;
(2)若DC=4,AC=6,求圆心O到AD的距离;
(3)若tan∠DAC=
| 2 |
| 3 |
| BE |
| BD |
考点:切线的判定,勾股定理,相似三角形的判定与性质
专题:
分析:(1)连接OD,根据AD平分∠BAC,∠BAD=∠DAC,由OA=OD,得∠BAD=∠ODA,可证明AC∥OD,则∠ODC=90°,即BC是⊙O的切线;
(2)在Rt△ADC中,∠ACD=90°,由勾股定理,得AD的长,作OF⊥AD于F,根据垂径定理得AF,可证△AOF∽△ADC,则
=
,从而得出OF的长;
(3)连接ED,由AD平分,得∠BAD=∠DAC,在Rt△AED中,由tan∠EAD=
=tan∠DAC=
,证明△BED∽△BDA,得
=
=
.
(2)在Rt△ADC中,∠ACD=90°,由勾股定理,得AD的长,作OF⊥AD于F,根据垂径定理得AF,可证△AOF∽△ADC,则
| OF |
| DC |
| AF |
| AC |
(3)连接ED,由AD平分,得∠BAD=∠DAC,在Rt△AED中,由tan∠EAD=
| ED |
| AD |
| 2 |
| 3 |
| BE |
| BD |
| DE |
| AD |
| 2 |
| 3 |
解答: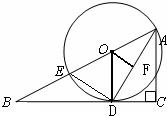 解:(1)连接OD,
解:(1)连接OD,
∵AD平分∠BAC,
∴∠BAD=∠DAC,
∵OA=OD,
∴∠BAD=∠ODA,
∴∠ODA=∠DAC,
∴AC∥OD,
∵∠C=90°,
∴∠ODC=90°,
即BC是⊙O的切线.
(2)在Rt△ADC中,∠ACD=90°,由勾股定理,
得:AD=
=
=2
,
作OF⊥AD于F,根据垂径定理得AF=
AD=
可证△AOF∽△ADC
∴
=
∴
=
∴OF=
;
(3)连接ED,
∵AD平分∠BAC,
∴∠BAD=∠DAC,
∵AE为直径,
∴∠ADE=90°,
∴在Rt△AED中,tan∠EAD=
=tan∠DAC=
,
∵∠AED=90°,
∴∠EDB+∠ADC=90°,
∵∠DAC+∠ADC=90°,
∴∠EDB=∠DAC=∠EAD,
∵∠B=∠B,
∴△BED∽△BDA,
∴
=
=
.
 解:(1)连接OD,
解:(1)连接OD,∵AD平分∠BAC,
∴∠BAD=∠DAC,
∵OA=OD,
∴∠BAD=∠ODA,
∴∠ODA=∠DAC,
∴AC∥OD,
∵∠C=90°,
∴∠ODC=90°,
即BC是⊙O的切线.
(2)在Rt△ADC中,∠ACD=90°,由勾股定理,
得:AD=
| AC2+DC2 |
| 62+42 |
| 13 |
作OF⊥AD于F,根据垂径定理得AF=
| 1 |
| 2 |
| 13 |
可证△AOF∽△ADC
∴
| OF |
| DC |
| AF |
| AC |
| OF |
| 4 |
| ||
| 6 |
∴OF=
| 2 |
| 3 |
| 13 |
(3)连接ED,
∵AD平分∠BAC,
∴∠BAD=∠DAC,
∵AE为直径,
∴∠ADE=90°,
∴在Rt△AED中,tan∠EAD=
| ED |
| AD |
| 2 |
| 3 |
∵∠AED=90°,
∴∠EDB+∠ADC=90°,
∵∠DAC+∠ADC=90°,
∴∠EDB=∠DAC=∠EAD,
∵∠B=∠B,
∴△BED∽△BDA,
∴
| BE |
| BD |
| DE |
| AD |
| 2 |
| 3 |
点评:本题考查了切线的判定、勾股定理以及相似三角形的判定和性质,是中考常见题型,要熟练掌握.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
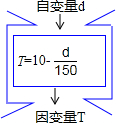 地球某地,温度T(℃)与高度d(m)的关系可以近似地用T=10-
地球某地,温度T(℃)与高度d(m)的关系可以近似地用T=10-| d |
| 150 |
| A、4℃ | B、5℃ | C、6℃ | D、16℃ |
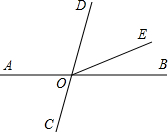 已知如图,直线AB、CD相交于点O,∠AOC=70°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,则∠AOE=( )
已知如图,直线AB、CD相交于点O,∠AOC=70°,OE把∠BOD分成两部分,且∠BOE:∠EOD=2:3,则∠AOE=( )| A、162° | B、152° |
| C、142° | D、132° |