题目内容
①先化简,再求值:3(x-1)(x-2)-3x(x+3),其中x=
.
②若关于x,y的二元一次方程组
的解满足x+y<2,试求a的取值范围.
| 1 |
| 3 |
②若关于x,y的二元一次方程组
|
考点:整式的混合运算—化简求值,二元一次方程组的解,解一元一次不等式
专题:
分析:①先根据多项式与多项式的乘法、单项式与多项式的乘法计算、再合并同类项,最后代入求值即可求解;
②两式相加,用a的代数式分别表示x+y的值,再代入x+y<2,求出a的取值范围.
②两式相加,用a的代数式分别表示x+y的值,再代入x+y<2,求出a的取值范围.
解答:解:①3(x-1)(x-2)-3x(x+3)
=3x2-9x+6-3x2-9x
=-18x+6,
把x=
代入,原式=-6+6=0.
②方程组
两式相加,
得4x+4y=4-a,
x+y=1-
a,
代入x+y<2,得1-
a<2,
解得a>-4.
所以m的取值范围a>-4.
=3x2-9x+6-3x2-9x
=-18x+6,
把x=
| 1 |
| 3 |
②方程组
|
得4x+4y=4-a,
x+y=1-
| 1 |
| 4 |
代入x+y<2,得1-
| 1 |
| 4 |
解得a>-4.
所以m的取值范围a>-4.
点评:①考查了整式的混合运算.主要考查了多项式与多项式的乘法、单项式与多项式的乘法、合并同类项的知识点.注意运算顺序以及符号的处理.
②考查了解一元一次不等式,所谓“方程组”的解,指的是该数值满足方程组中的每一方程的值.此类问题应先用a的代数式分别表示x,y的值,再列关于a的不等式求解集.
②考查了解一元一次不等式,所谓“方程组”的解,指的是该数值满足方程组中的每一方程的值.此类问题应先用a的代数式分别表示x,y的值,再列关于a的不等式求解集.

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
下列调查中,适合用普查方法的是( )
| A、了解某班学生对“北京精神”的知晓率 |
| B、了解某种奶制品中蛋白质的含量 |
| C、了解北京台《北京新闻》栏目的收视率 |
| D、了解一批科学计算器的使用寿命 |
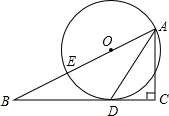 如图,已知点E在△ABC的边AB上,∠C=90°,∠BAC的平分线交BC于点D,且D在以AE为直径的⊙O上.
如图,已知点E在△ABC的边AB上,∠C=90°,∠BAC的平分线交BC于点D,且D在以AE为直径的⊙O上. (1)解分式方程:
(1)解分式方程: