题目内容
11.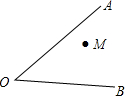 如图,在∠ABC内有一点M.
如图,在∠ABC内有一点M.(1)分别画出点M关于OA、0B的对称点M1、M2,连接M1M2,交0A于点P,交OB于点Q;
(2)在(1)的条件下,若M1M2=10cm,则△MPQ的周长为10cm;若∠A0B=50°,则∠M1OM2=100°;
(3)在OA、OB上分别任取点P′、Q′(不与点P、Q重合),连接MP′、P′Q′、MQ′,得到△MP′Q′,比较△MP′Q与△MPQ的周长,你得到什么结论?
分析 (1)利用关于直线对称点的图形的性质得出对应点位置,进而得出答案;
(2)利用轴对称变换的性质得出对应线段之间的关系,进而得出答案;
(3)利用(2)中所求得出△MPQ的周长面积最小,进而得出答案.
解答 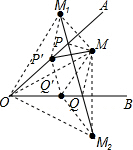 解:(1)如图所示:
解:(1)如图所示:
(2)∵点M关于OA,0B的对称点M1,M2,
∴M1P=PM,QM=QM2,
∴△MPQ的周长等于M1P+PQ+M2Q=M1M2=10cm;
∵MM1关于直线OA对称,MM2关于直线OB对称,
∴∠M1OM+∠M1OM=∠AOB=50°,
∴∠M1OM2=100°.
故答案为:10,100;
(3)如图所示:由△MPQ的周长等于M1M2,则此时△MPQ的周长面积最小,
△MP′Q′的周长为:M1P′+P′Q′+Q′M2,
故△MP′Q′大于△MPQ的周长
点评 此题主要考查了轴对称变换以及线段垂直平分线的性质,得出M1P=PM,QM=QM2是解题关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
1.绝对值不大于10.3的整数有( )
| A. | 10个 | B. | 11个 | C. | 20个 | D. | 21个 |
2.下列度数中,不可能是某个多边形的内角和的是( )
| A. | 180° | B. | 270° | C. | 2700° | D. | 1080° |
19.股民王海上星期六买进某公司的股票3000股,每股17元,下表为本周内每日股票的涨跌情况(单位:元)
试问:
(1)本周内,每股的最高价是多少元?最低价是多少元?分别是星期几?
(2)以上星期六为0点,画出本周内股票价格涨跌情况的折线图.

| 星期 | 一 | 二 | 三 | 四 | 五 | 六 |
| 每股涨跌 | +4 | +4.5 | -1 | -2.5 | -6 | +2 |
(1)本周内,每股的最高价是多少元?最低价是多少元?分别是星期几?
(2)以上星期六为0点,画出本周内股票价格涨跌情况的折线图.

3.已知二次函数y=x2+bx+c在1≤x≤5的范围内,当x=1时取得最大值,则b的取值范围是( )
| A. | b≤-6 | B. | b≤-5 | C. | b≥0 | D. | b≥3 |
 如图所示,已知:DE∥BC,∠DEB=∠GFC.求证:BE∥FG.
如图所示,已知:DE∥BC,∠DEB=∠GFC.求证:BE∥FG. 如图是某月的日历,现用一长方形在日历中任意框出4个数
如图是某月的日历,现用一长方形在日历中任意框出4个数 ,请用一个等式表示a,b,c,d之间的关系.
,请用一个等式表示a,b,c,d之间的关系. 如图,△ABD中,∠D=90°,E为AB上一点,AC=BC=BE,AE=CE,求∠DBC的度数.
如图,△ABD中,∠D=90°,E为AB上一点,AC=BC=BE,AE=CE,求∠DBC的度数.