题目内容
△ABC的三边长都是方程x2-6x+8=0的解,则△ABC的周长是( )
| A、10 |
| B、12 |
| C、6或10或12 |
| D、6或8或10或12 |
考点:解一元二次方程-因式分解法,三角形三边关系
专题:
分析:先求出方程的两个解,再分类讨论三角形三边长求解即可.
解答:解:解方程x2-6x+8=0得x1=2,x2=4,
当△ABC的三边长为2时,则△ABC的周长是6,
当△ABC的三边长为4时,则△ABC的周长是12,
当△ABC的一边长为2,其余两边长为4时,则△ABC的周长是10,
综上所述△ABC的周长是6或10或12.
故选:C.
当△ABC的三边长为2时,则△ABC的周长是6,
当△ABC的三边长为4时,则△ABC的周长是12,
当△ABC的一边长为2,其余两边长为4时,则△ABC的周长是10,
综上所述△ABC的周长是6或10或12.
故选:C.
点评:本题主要考查了解一元二次方程及三角形三边关系.解题的关键是确定三角形的三条边的长.

练习册系列答案
相关题目
已知关于x的方程mx2-2(m-1)x+(m-1)=0有实根,则m的取值范围是( )
| A、m>1 | B、m≥1 |
| C、m≤1 | D、m≤1且m≠0 |
下列方程中是一元二次方程的有( )
①4x2=x ②2x2xy+4=0 ③x2=0 ④
-
=2 ⑤6x(x-5)=6x2.
①4x2=x ②2x2xy+4=0 ③x2=0 ④
| 1 |
| x2 |
| 1 |
| x |
| A、2个 | B、3个 | C、4个 | D、5个 |
下列方程中,是二元一次方程的是( )
| A、3x-2y=4z | ||
| B、6xy+9=0 | ||
C、
| ||
| D、4x=y-2 |
下列各组式中是同类项的为( )
| A、4x3y与-2xy3 |
| B、-4yx与7xy |
| C、9xy与-3x2 |
| D、ab与bc |
 如图,AB∥CD,AE交CD于C,∠A=34°,∠DEC=90°,则∠D的度数为
如图,AB∥CD,AE交CD于C,∠A=34°,∠DEC=90°,则∠D的度数为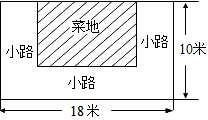 如图,池塘边有一块长为18米,宽为10米的长方形土地,现在将其余三面留出宽都是x米小路,中间余下长方形部分做菜地.
如图,池塘边有一块长为18米,宽为10米的长方形土地,现在将其余三面留出宽都是x米小路,中间余下长方形部分做菜地. A、B两点在直线c的两侧,在c上找一点P,使点P到A、B的距离之差最大,写出作法,并说明理由.
A、B两点在直线c的两侧,在c上找一点P,使点P到A、B的距离之差最大,写出作法,并说明理由.