题目内容
问题解决
如图(1),已知,在等腰直角△ABC中,∠BAC=90°,点D在BC上.以AD为边作正方形ADEF,连接CF.求证:CF=BD;
问题变式
如图(2),当点D在线段BC的延长线上时,其它条件不变,猜想CF、BC、CD三条线段之间的关系并说明理由;
问题拓展
如图(3),已知,点D是等边△ABC的边BC延长线上的一点,连接AD,以AD为边作菱形ADEF,并且使∠FAD=60°,CF垂直平分AD,猜想CG与FG之间的数量关系并证明你的结论.
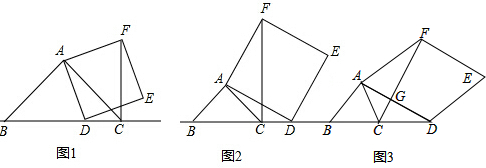
如图(1),已知,在等腰直角△ABC中,∠BAC=90°,点D在BC上.以AD为边作正方形ADEF,连接CF.求证:CF=BD;
问题变式
如图(2),当点D在线段BC的延长线上时,其它条件不变,猜想CF、BC、CD三条线段之间的关系并说明理由;
问题拓展
如图(3),已知,点D是等边△ABC的边BC延长线上的一点,连接AD,以AD为边作菱形ADEF,并且使∠FAD=60°,CF垂直平分AD,猜想CG与FG之间的数量关系并证明你的结论.

考点:全等三角形的判定与性质,等腰直角三角形,正方形的性质
专题:
分析:(1)根据等腰直角三角形的性质可得∠ABC=∠ACB=45°,再根据正方形的性质可得AD=AF,∠DAF=90°,然后利用同角的余角相等求出∠BAD=∠CAF,然后利用“边角边”证明△BAD和△CAF全等,从而得证;
(2)与(1)同理可得BD=CF,从而求出CF=BC+CD;
(3)依据线段的垂直平分线的性质得出AC=DC,从而得出∠CAD=30°,得出∠CAF=90°,然后根据30°角所对的直角边等于斜边的一半,即可求得.
(2)与(1)同理可得BD=CF,从而求出CF=BC+CD;
(3)依据线段的垂直平分线的性质得出AC=DC,从而得出∠CAD=30°,得出∠CAF=90°,然后根据30°角所对的直角边等于斜边的一半,即可求得.
解答:(1)证明:∵∠BAC=90°,AB=AC,
∴∠ABC=∠ACB=45°,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAC=∠BAD+∠DAC=90°,
∠DAF=∠CAF+∠DAC=90°,
∴∠BAD=∠CAF,
在△BAD和△CAF中,
,
∴△BAD≌△CAF(SAS),
∴CF=BD.
(2)CF=BC-CD,
理由:∵∠BAC=∠DAF=90°,
∴∠BAC+∠CAD=∠DAF+∠CAD,
即∠BAD=∠CAF,
在△BAD于△CAF中
∴△BAD≌△CAF(SAS)
∴AD=CF,
∴CF=BC+CD.
(3)CG=
GF,
∵CF垂直平分AD,
∴AC=DC,
∴∠CAD=∠CDA,
在等边△ABC中∠ACB=60°,
∴∠CAD=∠CDA=30°,
∴在RT△ACG中,CG=
AC
∵∠FAD=60°,
∴∠AFG=30°,
∴∠CAF=90°,
∴在RTACF中,AC=
CF,
∴CG=
CF,
∴CG=
FG.
∴∠ABC=∠ACB=45°,
∵四边形ADEF是正方形,
∴AD=AF,∠DAF=90°,
∵∠BAC=∠BAD+∠DAC=90°,
∠DAF=∠CAF+∠DAC=90°,
∴∠BAD=∠CAF,
在△BAD和△CAF中,
|
∴△BAD≌△CAF(SAS),
∴CF=BD.
(2)CF=BC-CD,
理由:∵∠BAC=∠DAF=90°,
∴∠BAC+∠CAD=∠DAF+∠CAD,
即∠BAD=∠CAF,
在△BAD于△CAF中
|
∴△BAD≌△CAF(SAS)
∴AD=CF,
∴CF=BC+CD.
(3)CG=
| 1 |
| 3 |
∵CF垂直平分AD,
∴AC=DC,
∴∠CAD=∠CDA,
在等边△ABC中∠ACB=60°,
∴∠CAD=∠CDA=30°,
∴在RT△ACG中,CG=
| 1 |
| 2 |
∵∠FAD=60°,
∴∠AFG=30°,
∴∠CAF=90°,
∴在RTACF中,AC=
| 1 |
| 2 |
∴CG=
| 1 |
| 4 |
∴CG=
| 1 |
| 3 |
点评:本题考查了正方形的性质,等腰直角三角形的性质,等边三角形的性质,全等三角形的判定与性质,线段的垂直平分线的性质以及30°角所对的直角边等于斜边的一半.(3)得出∠CAF=90°是本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目

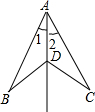 如图所示,已知∠1=∠2,请你添加一个条件,证明:AB=AC.
如图所示,已知∠1=∠2,请你添加一个条件,证明:AB=AC. 如图,等腰梯形ABCD中,如果AD∥BC,BD平分∠ABC,AD=2,∠C=60°,则BC=
如图,等腰梯形ABCD中,如果AD∥BC,BD平分∠ABC,AD=2,∠C=60°,则BC=