Question

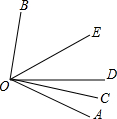如图，OC是∠AOD的平分线，OE是∠BOD的平分线．
（1）如果∠AOB=130°，那么∠COE是多少度？
（2）在（1）的条件下，如果∠COD=20°31′，那么∠BOE是多少度？

Answer 1

考点：角的计算,度分秒的换算,角平分线的定义

专题：

分析：（1）由OC是∠AOD的平分线，OE是∠BOD的平分线，可得∠COE=

1

2

∠AOB，然后将∠AOB=130°代入即可；
（2）由∠BOE=∠EOD=∠EOC-COD，然后将∠COD=20°31′，∠COE的度数代入即可．

解答：解：（1）∵OC是∠AOD的平分线，OE是∠BOD的平分线，
∴∠COD=∠AOC=

1

2

∠AOD，∠DOE=∠BOE=

1

2

∠BOD，
∴∠COE=∠COD+∠DOE
=

1

2

∠AOD+

1

2

∠BOD
=

1

2

×(∠AOD+∠BOD)
=

1

2

∠AOB
=

1

2

×130°
=65°；
（2）∵∠COD=20°31′，∠COE=65°，∠DOE=∠COE-∠COD，
∴∠DOE=65°-20°31′=44°29′，
∵∠BOE=∠DOE，
∴∠BOE=44°29′．

点评：此题考查了角的计算，解题的关键是：由角平分线的定义得到∠COE=

1

2

∠AOB．