题目内容
如图,将边长为3+ 的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=1,则重叠部分的面积为 .
的等边△ABC折叠,折痕为DE,点B与点F重合,EF和DF分别交AC于点M、N,DF⊥AB,垂足为D,AD=1,则重叠部分的面积为 .
【答案】分析:观察图形可知重叠部分的面积即是△DEF的面积减去△MNF的面积.由折叠的性质,可求得∠BDE=∠EDF=45°,由四边形的内角和为360°,求得∠BEF为150°,得到∠CEM为30°,则可证得∠EMC为90°;作△BDE的高,根据45°与60°的三角函数,借助于方程即可求得其高的值,则各三角形的面积可解.
解答:解:过点E作EG⊥AB于G,

∴∠EGB=90°,
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=AC=3+ ,
,
根据题意得:∠BDE=∠FDE,∠F=∠B=60°,
∵DF⊥AB,
∴∠FDB=90°,
∴∠BEF=360°-∠B-∠F-∠BDF=150°,∠BDE=∠FDE= ∠FDB=45°
∠FDB=45°
∴∠MEC=180°-∠BEF=30°,
∴∠EMC=180°-∠C-∠EMC=90°,
在Rt△ADN中,AD=1,tan∠A=tan60°= =
= ,
,
∴DN= ,
,
∴S△ADN= AD•DN=
AD•DN= ×1×
×1× =
= ,
,
在△BDE中,DB=AB-AD=3+ -1=2+
-1=2+ ,
,
∵∠EDG=45°,
∴∠DEG=45°,
∴DG=EG,
∵tan∠B=tan60°= =
= ,
,
设EG=x,则DG=x,BG= x,
x,
∴x+ x=2+
x=2+ ,
,
解得:x= ,
,
∴EG=DG= ,
,
∴S△BDE= BD•EG=
BD•EG= ×(2+
×(2+ )×
)× =
= ,
,
∵∠B=∠C=∠F=60°,
∴BE= =
= +1,
+1,
∴EC=BC-BE=2,
∵∠BED=∠FED=180°-∠B-∠BDE=75°,
∴∠FNM=∠MEC=30°,
∴∠FMN=∠EMC=90°,
∴EM=EC•cos30°= ,
,
∴FM=EF-EM=BE-EM=1,
∴MN=FM•tan60°= ,
,
∴S四边形MNDE=S△DEF-S△MNF=S△BDE-S△MNF= -
- ×1×
×1× =
= .
.
点评:此题考查了等边三角形的性质,折叠的性质以及三角函数的性质等知识.此题综合性很强,解题的关键是抓住数形结合思想的应用.
解答:解:过点E作EG⊥AB于G,

∴∠EGB=90°,
∵△ABC是等边三角形,
∴∠A=∠B=∠C=60°,AB=BC=AC=3+
 ,
,根据题意得:∠BDE=∠FDE,∠F=∠B=60°,
∵DF⊥AB,
∴∠FDB=90°,
∴∠BEF=360°-∠B-∠F-∠BDF=150°,∠BDE=∠FDE=
 ∠FDB=45°
∠FDB=45°∴∠MEC=180°-∠BEF=30°,
∴∠EMC=180°-∠C-∠EMC=90°,
在Rt△ADN中,AD=1,tan∠A=tan60°=
 =
= ,
,∴DN=
 ,
,∴S△ADN=
 AD•DN=
AD•DN= ×1×
×1× =
= ,
,在△BDE中,DB=AB-AD=3+
 -1=2+
-1=2+ ,
,∵∠EDG=45°,
∴∠DEG=45°,
∴DG=EG,
∵tan∠B=tan60°=
 =
= ,
,设EG=x,则DG=x,BG=
 x,
x,∴x+
 x=2+
x=2+ ,
,解得:x=
 ,
,∴EG=DG=
 ,
,∴S△BDE=
 BD•EG=
BD•EG= ×(2+
×(2+ )×
)× =
= ,
,∵∠B=∠C=∠F=60°,
∴BE=
 =
= +1,
+1,∴EC=BC-BE=2,
∵∠BED=∠FED=180°-∠B-∠BDE=75°,
∴∠FNM=∠MEC=30°,
∴∠FMN=∠EMC=90°,
∴EM=EC•cos30°=
 ,
,∴FM=EF-EM=BE-EM=1,
∴MN=FM•tan60°=
 ,
,∴S四边形MNDE=S△DEF-S△MNF=S△BDE-S△MNF=
 -
- ×1×
×1× =
= .
.点评:此题考查了等边三角形的性质,折叠的性质以及三角函数的性质等知识.此题综合性很强,解题的关键是抓住数形结合思想的应用.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
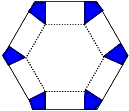 如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为
如图,将边长为6cm的正六边形纸板的六个角各剪切去一个全等的四边形,再沿虚线折起,做成一个无盖直六棱柱纸盒,使侧面积等于底面积,被剪去的六个四边形的面积和为 12、如图,将边长为12cm的正方形纸片ABCD折叠,使得点A落在边CD上的E点,折痕为MN,若MN的长为13cm,则CE的长为( )
12、如图,将边长为12cm的正方形纸片ABCD折叠,使得点A落在边CD上的E点,折痕为MN,若MN的长为13cm,则CE的长为( )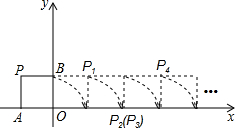 如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2009次,点P依次落在点P1,P2,P3,P4,…,P2009的位置,则P2009的坐标为
如图,将边长为1的正方形OAPB沿x轴正方向连续翻转2009次,点P依次落在点P1,P2,P3,P4,…,P2009的位置,则P2009的坐标为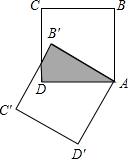 如图,将边长为
如图,将边长为 如图,将边长为3cm的正方形ABCD绕点C逆时针旋转30°后得到正方形A′B′C D′,那么图中阴影部分面积为( )
如图,将边长为3cm的正方形ABCD绕点C逆时针旋转30°后得到正方形A′B′C D′,那么图中阴影部分面积为( )