题目内容
3.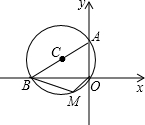 如图,⊙C过原点O,且与两坐标轴分别交于点A、B,点A的坐标为(0,4),点M是第三象限内$\widehat{OB}$上一点,∠BMO=120°,则⊙O的半径为( )
如图,⊙C过原点O,且与两坐标轴分别交于点A、B,点A的坐标为(0,4),点M是第三象限内$\widehat{OB}$上一点,∠BMO=120°,则⊙O的半径为( )| A. | 4 | B. | 5 | C. | 6 | D. | 2$\sqrt{3}$ |
分析 连接OC,由圆周角定理可知AB为⊙C的直径,再根据∠BMO=120°可求出∠BAO的度数,证明△AOC是等边三角形,即可得出结果.
解答 解:连接OC,如图所示:
∵∠AOB=90°,
∴AB为⊙C的直径,
∵∠BMO=120°,
∴∠BCO=120°,∠BAO=60°,
∵AC=OC,∠BAO=60°,
∴△AOC是等边三角形,
∴⊙C的半径=OA=4.
故选:A.
点评 本题考查了圆周角定理、圆内接四边形的性质、等边三角形的判定与性质;熟练掌握圆内接四边形的性质,证明三角形是等边三角形是解决问题的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
18.抛物线y=(x+1)2+1的顶点坐标是( )
| A. | (1,1) | B. | (-1,1) | C. | (1,-1) | D. | (-1,-1) |
8.已知y(y-16)+a=(y-8)2,则a的值是( )
| A. | 8 | B. | 16 | C. | 32 | D. | 64 |
15.开口向下的抛物线的顶点P的坐标是(1,-3),则此抛物线对应的二次函数有( )
| A. | 最大值1 | B. | 最小值-1 | C. | 最大值-3 | D. | 最小值3 |
13.数轴上的两点A、B分别表示-2,3,则点A、B间的距离为( )
| A. | -1 | B. | 1 | C. | -5 | D. | 5 |