题目内容

14．一个多边形的内角和是外角和的一半，它是几边形？

分析 多边形的外角和是360°，多边形的内角和是外角和的一半，则多边形的内角和是180°，根据多边形的内角和可以表示成（n-2）•180°，依此列方程可求解．

解答 解：设多边形边数为n．
则360°=2×（n-2）•180°，
解得n=3．
则多边形为三角形．

点评 本题主要考查了多边形内角和公式及外角的特征．解决本题的关键是求多边形的边数，可以转化为方程的问题来解决．

练习册系列答案
相关题目
4．已知△ABC≌△A′B′C′，且AB=2cm，则A′B′的长为2 cm．
5．如图，点A，B在数轴上表示的数分别为a，b，下列式子成立的是（　　）
A．a+b＞0B．a-b＞0C．ab＞0D．a3＞0
2．如图①、图②，在4×6的正方形网格中，每个小正方形的边长均为1，每个小正方形的顶点叫做格点．△ABC的顶点在格点上，在图①、图②两个网格中画出一个与△ABC相似的三角形．要求：所画的三角形的顶点在格点上，与△ABC有公共点B，且与△ABC的相似比不为1．
9．观察解方程$\frac{3}{2}$|x+5|=5的过程，然后解方程．
分析：将|x+5|作为一个整体求值，再根据绝对值的定义去掉绝对值符号．
解：由原方程得|x+5|=$\frac{10}{3}$．
由绝对值的定义可知：x+5=$\frac{10}{3}$或x+5=-$\frac{10}{3}$．
所以x=-1$\frac{2}{3}$或x=-8$\frac{1}{3}$
解方程：$\frac{2}{3}$|2x-3|=4．
19．某种零件，标明加工要求是φ20±0.02mm（φ表示直径，单位：毫米），+0.02和-0.02表示直径在（20+0.02）mm到（20-0.02）mm之间的产品都属于合格产品．经检查，一个零件的直径是19.9mm，该零件不合格（填“合格”或“不合格”）．
6．-$\frac{1}{2}$的相反数是$\frac{1}{2}$，-3的倒数是-$\frac{1}{3}$，-1.8的绝对值是1.8．
3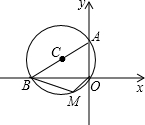．如图，⊙C过原点O，且与两坐标轴分别交于点A、B，点A的坐标为（0，4），点M是第三象限内$\widehat{OB}$上一点，∠BMO=120°，则⊙O的半径为（　　）
A．4B．5C．6D．2$\sqrt{3}$
4．（1）$（3{x^2}y-x{y^2}+2xy）÷\frac{1}{2}xy$
（2）（ab2）2•（-a3b）3÷（-5ab）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网