题目内容
13.在等腰△ABC中,AB=AC,∠BAC=120°,点D在直线BC上,且CD=AB,则∠BAD=45°或135°.分析 首先根据题意画出图形,然后利用等腰三角形的性质求解即可求得答案,注意分为点D在边BC上或在BC的延长线上.
解答 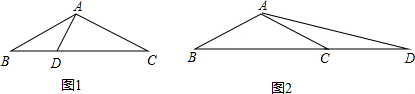 解:如图1,∵在等腰△ABC中,AB=AC,∠BAC=120°,
解:如图1,∵在等腰△ABC中,AB=AC,∠BAC=120°,
∴∠B=∠C=30°,
∵CD=AB,
∴CD=AC,
∴∠CAD=∠CDA=$\frac{180°-∠C}{2}$=75°,
∴∠BAD=∠BAC-∠CAD=45°;
如图2,在等腰△ABC中,AB=AC,∠BAC=120°,
∴∠B=∠ACB=30°,
∵CD=AB,
∴CD=AC,
∴∠CAD=∠D=$\frac{1}{2}$∠ACB=15°,
∴∠BAD=∠BAC+∠CAD=135°;
综上所述:∠BAD=35°或135°.
故答案为:45°或135°.
点评 此题考查了等腰三角形的性质.注意结合题意画出图形,利用图形求解是关键.

练习册系列答案
相关题目
5. 如图,点A,B在数轴上表示的数分别为a,b,下列式子成立的是( )
如图,点A,B在数轴上表示的数分别为a,b,下列式子成立的是( )
 如图,点A,B在数轴上表示的数分别为a,b,下列式子成立的是( )
如图,点A,B在数轴上表示的数分别为a,b,下列式子成立的是( )| A. | a+b>0 | B. | a-b>0 | C. | ab>0 | D. | a3>0 |
3.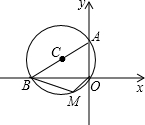 如图,⊙C过原点O,且与两坐标轴分别交于点A、B,点A的坐标为(0,4),点M是第三象限内$\widehat{OB}$上一点,∠BMO=120°,则⊙O的半径为( )
如图,⊙C过原点O,且与两坐标轴分别交于点A、B,点A的坐标为(0,4),点M是第三象限内$\widehat{OB}$上一点,∠BMO=120°,则⊙O的半径为( )
 如图,⊙C过原点O,且与两坐标轴分别交于点A、B,点A的坐标为(0,4),点M是第三象限内$\widehat{OB}$上一点,∠BMO=120°,则⊙O的半径为( )
如图,⊙C过原点O,且与两坐标轴分别交于点A、B,点A的坐标为(0,4),点M是第三象限内$\widehat{OB}$上一点,∠BMO=120°,则⊙O的半径为( )| A. | 4 | B. | 5 | C. | 6 | D. | 2$\sqrt{3}$ |
 如图,把长方形ABCD沿EF对折,若∠1=52°,则∠AEF的度数等于116°.
如图,把长方形ABCD沿EF对折,若∠1=52°,则∠AEF的度数等于116°.