题目内容
12. 如图,已知△ABC,∠A=52°,OB、OC是∠ABC和∠ACB的平分线,则∠BOC=116°.
如图,已知△ABC,∠A=52°,OB、OC是∠ABC和∠ACB的平分线,则∠BOC=116°.
分析 根据三角形的角平分线定义和三角形的内角和定理,求出∠OBC+∠OCB的度数,再根据三角形的内角和定理,即可求出∠BOC的度数.
解答 解:∵OB、OC分别是∠ABC和∠ACB的角平分线,
∴∠OBC+∠OCB=$\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB=$\frac{1}{2}$(∠ABC+∠ACB),
∵∠A=52°,
∴∠OBC+∠OCB=$\frac{1}{2}$(180°-52°)=64°,
∴∠BOC=180°-(∠OBC+∠OCB)
=180°-64°
=116°.
故答案为:116°
点评 本题主要利用角平分线的定义和三角形内角和定理求解,熟记概念和定理是解题的关键.

练习册系列答案
相关题目
3.几何体的下列性质:①侧面是平行四边形;②底面形状相同;③底面平行;④棱长相等.其中棱柱具有的性质有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8.动点M从点A出发,以每秒1个单位长度的速度沿AB向点B匀速运动;同时,动点N从点B出发,以每秒3个单位长度的速度沿BA向点A匀速运动.过线段MN的中点G作边AB的垂线,垂足为点G,交△ABC的另一边于点P,连接PM、PN,当点N运动到点A时,M、N两点同时停止运动,设运动时间为t秒.
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8.动点M从点A出发,以每秒1个单位长度的速度沿AB向点B匀速运动;同时,动点N从点B出发,以每秒3个单位长度的速度沿BA向点A匀速运动.过线段MN的中点G作边AB的垂线,垂足为点G,交△ABC的另一边于点P,连接PM、PN,当点N运动到点A时,M、N两点同时停止运动,设运动时间为t秒.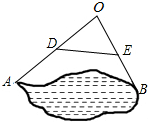
 如图所示,已知抛物线y=-2x2-4x的图象E,将其向右平移两个单位后得到图象F.求图象F所表示的抛物线的解析式.
如图所示,已知抛物线y=-2x2-4x的图象E,将其向右平移两个单位后得到图象F.求图象F所表示的抛物线的解析式.