题目内容
15.已知实数a、b满足(a-b+$\sqrt{3}$)2+(a+b-2)2=0,则a2-b2=-2$\sqrt{3}$,a2+b2=$\frac{7}{2}$,ab=$\frac{1}{4}$.分析 根据非负数的性质得到a-b=-$\sqrt{3}$,a+b=2,然后利用平方差公式,完全平方公式进行解答即可.
解答 解:∵(a-b+$\sqrt{3}$)2+(a+b-2)2=0,
∴a-b+$\sqrt{3}$=0,a+b-2,
∴a-b=-$\sqrt{3}$,a+b=2,
∴a2-b2=(a-b)(a+b)=(-$\sqrt{3}$)×2=-2$\sqrt{3}$;
a2+b2=$\frac{1}{2}$[(a+b)2+(a-b)]2=$\frac{1}{2}$(4+3)=$\frac{7}{2}$;
ab=$\frac{1}{2}$[(a+b)2-(a2+b2)]=$\frac{1}{2}$(4-$\frac{7}{2}$)=$\frac{1}{4}$.
故答案是:-2$\sqrt{3}$;$\frac{7}{2}$;$\frac{1}{4}$.
点评 本题考查了完全平方公式,非负数的性质.熟记公式的几个变形公式对解题大有帮助.

练习册系列答案
相关题目
4.已知正比例函数y=(k-2)x的图象位于第二、第四象限,则k的取值范围是( )
| A. | k>2 | B. | k≥2 | C. | k≤2 | D. | k<2 |
 如图,已知直线a,b,c两两相交,∠1=2∠3,∠2=84°,求∠4的度数.
如图,已知直线a,b,c两两相交,∠1=2∠3,∠2=84°,求∠4的度数.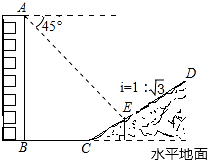 如图,一楼房AB后有一假山,其坡度为i=1:$\sqrt{3}$,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=26米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°.(注:坡度i是指坡面的铅直高度与水平宽度的比)
如图,一楼房AB后有一假山,其坡度为i=1:$\sqrt{3}$,山坡坡面上E点处有一休息亭,测得假山坡脚C与楼房水平距离BC=26米,与亭子距离CE=18米,小丽从楼房顶测得E点的俯角为45°.(注:坡度i是指坡面的铅直高度与水平宽度的比)