题目内容
9.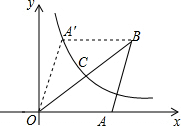 如图,在平面直角坐标系中,△OAB的边OA在x轴的正半轴上,OA=AB,边OB的中点C在双曲线y=$\frac{k}{x}$上,将△OAB沿OB翻折后,点A的对应点A′,正好落在双曲线y=$\frac{k}{x}$上,△OAB的面积为6,则k为( )
如图,在平面直角坐标系中,△OAB的边OA在x轴的正半轴上,OA=AB,边OB的中点C在双曲线y=$\frac{k}{x}$上,将△OAB沿OB翻折后,点A的对应点A′,正好落在双曲线y=$\frac{k}{x}$上,△OAB的面积为6,则k为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 过点A′作A′E⊥x轴于点E,过点C作CF⊥x轴于点F,过点B作BM⊥x轴于点M,根据OA=AB结合翻折的特性可知∠A′BO=∠AOB,四边形OABA′为菱形,由菱形的性质结合点C为线段OB的中点可得出S△OA′E=S△ABM,再根据反比例函数系数k的几何意义和三角形面积公式即可得出$\frac{1}{2}$|k|=$\frac{1}{4}$(6+$\frac{1}{2}$|k|),解之结合反比例函数在第一象限有图象即可得出k值.
解答 解:过点A′作A′E⊥x轴于点E,过点C作CF⊥x轴于点F,过点B作BM⊥x轴于点M,如图所示.
∵OA=AB,
∴∠AOB=∠ABO,
由翻折的性质可知:∠A′BO=∠ABO,A′B=AB,A′O=AO,
∴∠A′BO=∠AOB,四边形OABA′为菱形,
∴A′B∥OA.
∵点C是线段OB的中点,A′E⊥x轴,CF⊥x轴,BM⊥x轴,
∴A′E=BM=2CF,OE=AM,OM=2OF,
∴S△OA′E=S△ABM.
∵点A′、C在反比例函数y=$\frac{k}{x}$上,
∴S△OCF=S△OA′E=$\frac{1}{2}$|k|=$\frac{1}{4}$S△OBM=$\frac{1}{4}$(S△OAB+S△ABM),即$\frac{1}{2}$|k|=$\frac{1}{4}$(6+$\frac{1}{2}$|k|),
解得:k=±4,
∵反比例函数在第一象限有图象,
∴k=4.
故选D.
点评 本题考查了反比例函数系数k的几何意义、菱形的判定、平行线的性质以及三角形的面积公式,根据反比例函数系数k的几何意义和三角形面积公式找出$\frac{1}{2}$|k|=$\frac{1}{4}$(6+$\frac{1}{2}$|k|)是解题的关键.

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案| A. | $\frac{2}{5}$ | B. | $\frac{1}{10}$ | C. | $\frac{4}{25}$ | D. | $\frac{1}{2}$ |

| A. | 8065 | B. | 8064 | C. | 8063 | D. | 8062 |
| 甲 | 0 | 2 | 3 | 0 | 1 |
| 乙 | 1 | 2 | 1 | 0 | 2 |
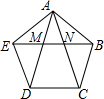 如图,在正五边形ABCDE中,对角线AD,AC与EB分别交于点M,N,则下列结论正确的是( )
如图,在正五边形ABCDE中,对角线AD,AC与EB分别交于点M,N,则下列结论正确的是( )| A. | EM:AE=2:$(\sqrt{5}-1)$ | B. | MN:EM=$(\sqrt{5}-1)$:$(3-\sqrt{5})$ | C. | AM:MN=$(3-\sqrt{5})$:$(\sqrt{5}-1)$ | D. | MN:DC=$(3-\sqrt{5})$:2 |
| A. | n边形的内角和等于(n-2)•180° | |
| B. | 边长分别为3,4,5,的三角形是直角三角形 | |
| C. | 垂直于弦的直径平分弦所对的两条弧 | |
| D. | 圆的切线垂直于半径 |
 小明上学期的数学成绩如表所示(单位:分)
小明上学期的数学成绩如表所示(单位:分)| 测验类别 | 平时 | 期中考试 | 期末考试 | |||
| 测试1 | 测试2 | 测试3 | 测试4 | |||
| 成绩 | 107 | 110 | 114 | 109 | 110 | 115 |
(2)计算小明上学期平时测试的数学平均成绩;
(3)如果上学期的数学总评成绩是根据如图所示的比例计算得到的,已知小明上学期的数学总评成绩为113分,那么请计算出数学总评成绩中期中、期末成绩各自所占的比例.
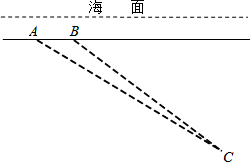 如图,一艘潜艇在海面下500m深的点A处,测得正前方俯角为31°方向上的海底有黑匣子发出信号,潜艇在同一深度保持直线航行500m,在点B处测得海底黑匣子位于正前方俯角36.9°的方向上,海底黑匣子C所在点距海面的深度为2000m.(精确到1,m.参考数据:sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75,sin31°≈0.51,cos31°≈0.87,tan31°≈0.60)
如图,一艘潜艇在海面下500m深的点A处,测得正前方俯角为31°方向上的海底有黑匣子发出信号,潜艇在同一深度保持直线航行500m,在点B处测得海底黑匣子位于正前方俯角36.9°的方向上,海底黑匣子C所在点距海面的深度为2000m.(精确到1,m.参考数据:sin36.9°≈0.60,cos36.9°≈0.80,tan36.9°≈0.75,sin31°≈0.51,cos31°≈0.87,tan31°≈0.60)