题目内容
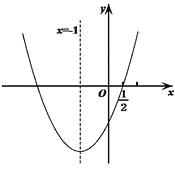
【题目】已知点![]() 为二次函数
为二次函数![]() 的图象的顶点.
的图象的顶点.
(1)过点![]() 作
作![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,求线段
,求线段![]() 的最小值;
的最小值;
(2)设正比例函数![]() 与上述二次函数的图象相交于点
与上述二次函数的图象相交于点![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() ,
,![]() 的值.
的值.
【答案】(1)PQ最小值为4;(2)k=2时m=-4;k=-2时,m=4.
【解析】
(1)将二次函救的解析式由一般式化为顶点式,用含![]() 的式子表示出顶点坐标,进而表示出线段
的式子表示出顶点坐标,进而表示出线段![]() 的长,并结合二次函数的性质求线段的最值;
的长,并结合二次函数的性质求线段的最值;
(2)易知点![]() ,
,![]() 关于原点对称,用含
关于原点对称,用含![]() 的式子表示出顶点
的式子表示出顶点![]() 的坐标后,根据对称性表示出点
的坐标后,根据对称性表示出点![]() 的坐标,将点
的坐标,将点![]() 的坐标代入二次函数的解析式求解即可得到
的坐标代入二次函数的解析式求解即可得到![]() 的值,进而得到点
的值,进而得到点![]() 的坐标,将点
的坐标,将点![]() 的坐标代入正比例函数的解析式即可得到
的坐标代入正比例函数的解析式即可得到![]() 的值.
的值.
(1)![]() ,
,![]() ,
,
![]() .
.
易得当![]() 时,
时,![]() 取得最小值,最小值为4.
取得最小值,最小值为4.
(2)![]() 是正比例函数,
是正比例函数,![]() ,
,
∴点![]() ,
,![]() 关于原点
关于原点![]() 对称,则
对称,则![]() .
.
将![]() 代入
代入![]() ,
,
得![]() ,解得
,解得![]() .
.
当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() .
.
∵点![]() 在正比例函数
在正比例函数![]() 的图象上,
的图象上,
![]()
当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() .
.
∵点![]() 在正比例函数
在正比例函数![]() 的图象上,
的图象上,
![]() .
.

【题目】某市A,B两个蔬菜基地得知四川C,D两个灾民安置点分别急需蔬菜240t和260t的消息后,决定调运蔬菜支援灾区,已知A蔬菜基地有蔬菜200t,B蔬菜基地有蔬菜300t,现将这些蔬菜全部调运C,D两个灾区安置点.从A地运往C,D两处的费用分别为每吨20元和25元,从B地运往C,D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
(1)请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值;
C | D | 总计/t | |
A | 200 | ||
B | x | 300 | |
总计/t | 240 | 260 | 500 |
(2)设A,B两个蔬菜基地的总运费为w元,求出w与x之间的函数关系式,并求
总运费最小的调运方案;
(3)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少m元(m>0),其余线路的运费不变,试讨论总运费最小的调动方案.