Question

17．如图，正方形ABCD内有两点E、F满足AE=1，EF=FC=3，AE⊥EF，CF⊥EF，则正方形ABCD的边长为（　　）

• A． 4
• B． $\frac{5}{2}\sqrt{2}$
• C． 4$\sqrt{2}$
• D． 5$\sqrt{2}$

Answer 1

分析 连接AC，交EF于点M，可证明△AEM∽△CMF，根据条件可求得AE、EM、FM、CF，再结合勾股定理可求得AB．

解答 解：连接AC，交EF于点M，
∵AE丄EF，EF丄FC，
∴∠E=∠F=90°，
∵∠AME=∠CMF，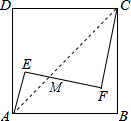
∴△AEM∽△CFM，
∴$\frac{AE}{CF}$=$\frac{EM}{FM}$，
∵AE=1，EF=FC=3，
∴$\frac{EM}{FM}$=$\frac{1}{3}$，
∴EM=$\frac{3}{4}$，FM=$\frac{9}{4}$，
在Rt△AEM中，AM²=AE²+EM²=1+$\frac{9}{16}$=$\frac{25}{16}$，解得AM=$\frac{5}{4}$，
在Rt△FCM中，CM²=CF²+FM²=9+$\frac{81}{16}$=$\frac{225}{16}$，解得CM=$\frac{15}{4}$，
∴AC=AM+CM=5，
在Rt△ABC中，AB=BC，AB²+BC²=AC²=25，
∴AB=$\frac{5\sqrt{2}}{2}$，即正方形的边长为$\frac{5\sqrt{2}}{2}$．
故选B．

点评 本题主要考查相似三角形的判定和性质及正方形的性质，构造三角形相似利用相似三角形的对应边成比例求得AC的长是解题的关键，注意勾股定理的应用．