题目内容
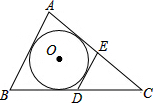 如图,⊙O为△ABC的内切圆,AC=10,AB=8,BC=9,点D,E分别为BC,AC上的点,且DE为⊙O的切线,则△CDE的周长为( )
如图,⊙O为△ABC的内切圆,AC=10,AB=8,BC=9,点D,E分别为BC,AC上的点,且DE为⊙O的切线,则△CDE的周长为( )| A、9 | B、7 | C、11 | D、8 |
考点:切线长定理
专题:
分析:设AB,AC,BC和圆的切点分别是P,N,M.根据切线长定理得到NC=MC,QE=DQ.所以三角形CDE的周长即是CM+CN的值,再进一步根据切线长定理由三角形ABC的三边进行求解即可.
解答: 解:设AB,AC,BC和圆的切点分别是P,N,M,CM=x,根据切线长定理,得
解:设AB,AC,BC和圆的切点分别是P,N,M,CM=x,根据切线长定理,得
CN=CM=x,BM=BP=9-x,AN=AP=10-x.
则有9-x+10-x=8,
解得:x=5.5.
所以△CDE的周长=CD+CE+QF+DQ=2x=11.
故选:C.
 解:设AB,AC,BC和圆的切点分别是P,N,M,CM=x,根据切线长定理,得
解:设AB,AC,BC和圆的切点分别是P,N,M,CM=x,根据切线长定理,得CN=CM=x,BM=BP=9-x,AN=AP=10-x.
则有9-x+10-x=8,
解得:x=5.5.
所以△CDE的周长=CD+CE+QF+DQ=2x=11.
故选:C.
点评:此题主要是考查了切线长定理.要掌握圆中的有关定理,才能灵活解题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 如图,在三角ABC中,延长BC至D,过C点作CE∥AB,请你用量角器量一量∠A与∠ACE的大小,∠B与∠ECD的大小,你发现了什么?
如图,在三角ABC中,延长BC至D,过C点作CE∥AB,请你用量角器量一量∠A与∠ACE的大小,∠B与∠ECD的大小,你发现了什么?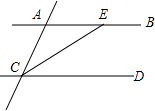 如图,AB∥CD,CE平分∠ACD,∠ACD=50°,求∠CEB的度数.
如图,AB∥CD,CE平分∠ACD,∠ACD=50°,求∠CEB的度数.