题目内容
已知△ABC的三边a、b、c,且a+b=17,ab=60,c=13,△ABC是否是直角三角形?你能说明理由吗?
考点:勾股定理的逆定理
专题:
分析:由a+b=17可得(a+b)2=a2+b2+2ab=172,求出a2+b2的值,与c2的值相比较,若相等,根据勾股定理的逆定理可得△ABC是直角三角形.
解答:解:△ABC是直角三角形.
理由:解:∵a+b=17,ab=60
∴(a+b)2=a2+b2+2ab=172,
∴a2+b2=172-2×60=169=c2,
所以,△ABC是直角三角形.
理由:解:∵a+b=17,ab=60
∴(a+b)2=a2+b2+2ab=172,
∴a2+b2=172-2×60=169=c2,
所以,△ABC是直角三角形.
点评:本题主要考查勾股定理的逆定理,根据题意由勾股定理的逆定理判断三角形的形状.解题的关键是:由a+b=17可得(a+b)2=a2+b2+2ab=172,进而求出a2+b2的值.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
下列根式中,最简二次根式是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,已知∠1=∠2,∠3=∠4,AD∥BC,试证明∠5=∠6.
如图,已知∠1=∠2,∠3=∠4,AD∥BC,试证明∠5=∠6.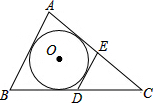 如图,⊙O为△ABC的内切圆,AC=10,AB=8,BC=9,点D,E分别为BC,AC上的点,且DE为⊙O的切线,则△CDE的周长为( )
如图,⊙O为△ABC的内切圆,AC=10,AB=8,BC=9,点D,E分别为BC,AC上的点,且DE为⊙O的切线,则△CDE的周长为( )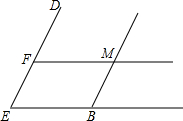 如图,已知AB∥DE,FM∥EC,∠ABC=65°,求∠EFM的度数.
如图,已知AB∥DE,FM∥EC,∠ABC=65°,求∠EFM的度数.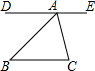 如图,直线DE经过点A,DE∥BC,∠B=44°,∠C=85°.
如图,直线DE经过点A,DE∥BC,∠B=44°,∠C=85°. 如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=3,CD=2.求AB的长.
如图,在四边形ABCD中,∠A=60°,∠B=∠D=90°,BC=3,CD=2.求AB的长. 如图所示,若AB∥CD,直线EF与AB、CD分别相交于点E,F,∠FEB与∠EFD的平分线相交于点P,且∠EFD=60°,求∠BEP的度数.
如图所示,若AB∥CD,直线EF与AB、CD分别相交于点E,F,∠FEB与∠EFD的平分线相交于点P,且∠EFD=60°,求∠BEP的度数.