题目内容
8.已知:四边形ABCD的对角线AC、BD相交于点O,给出下列4个条件:①AB∥CD;②OA=OC;③AB=CD;④AD∥BC从中任取两个条件,能推出四边形ABCD是平行四边形的概率是$\frac{1}{2}$.分析 首先根据题意画出树状图,然后由树状图求得所有等可能的结果与能推出四边形ABCD是平行四边形的情况,再利用概率公式即可求得答案.
解答 解:画树状图得: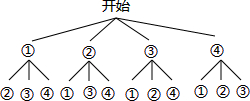
∵共有12种等可能的结果,能推出四边形ABCD是平行四边形的有6种情况,
∴能推出四边形ABCD是平行四边形的概率是:$\frac{6}{12}$=$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目
19.某小区开展“节约用水,从我做起”活动,下表是从该小区抽取的10个家庭与上月比较的一个月的节水情况统计:
那么这10个家庭的节水量(m3)的平均数和中位数分别是( )
| 节水量(m3) | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
| 家庭数(个) | 1 | 2 | 2 | 4 | 1 |
| A. | 0.42和0.4 | B. | 0.4和0.4 | C. | 0.42和0.45 | D. | 0.4和0.45 |
13.不等式组$\left\{\begin{array}{l}{x>4}\\{x>m}\end{array}\right.$的解集是x>4,那么m的取值范围是( )
| A. | m≥4 | B. | m≤4 | C. | 3≤x<4 | D. | 3<x≤4 |
20.一元二次方程x2-x-2=0的根的情况是( )
| A. | 有两个不相等的实数根 | B. | 有两个相等的实数根 | ||
| C. | 只有一个实数根 | D. | 没有实数根 |
17.下列命题中是假命题的是( )
| A. | 一个三角形中至少有两个锐角 | |
| B. | 在同一平面内,垂直于同一直线的两条直线平行 | |
| C. | 同角的补角相等 | |
| D. | 如果a为实数,那么|a|>0 |
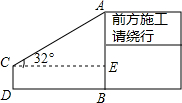 如图,为了测量某交通路口设立的路况显示牌的立杆AB的高度,在D处用高1.2m的测角仪CD,测得最高点A的仰角为32°,已知观测点D到立杆AB的距离DB为3.8m,求立杆AB的高度.(结果精确到0.1m)
如图,为了测量某交通路口设立的路况显示牌的立杆AB的高度,在D处用高1.2m的测角仪CD,测得最高点A的仰角为32°,已知观测点D到立杆AB的距离DB为3.8m,求立杆AB的高度.(结果精确到0.1m)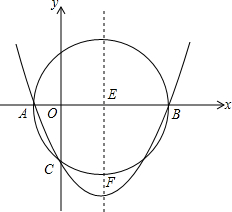 如图,己知以E(3,0)为圆心,以5为半径的⊙E与x轴交于A、B两点,与y轴交于点C,抛物线y=ax2+bx+c经过A、B、C三点,顶点为F.
如图,己知以E(3,0)为圆心,以5为半径的⊙E与x轴交于A、B两点,与y轴交于点C,抛物线y=ax2+bx+c经过A、B、C三点,顶点为F.