题目内容
15.甲乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案,在甲商场累计购物超过200元后,超出200元的部分按85%收费,在乙商店累计超过100元后,超出部分按照90%收费.(1)若小明妈妈准备用160元去购物,你建议小明妈妈去乙商场花费少(直接写出“甲”或“乙”);
(2)设顾客累计了购物花费x(x>200)元,若在甲商场购物,则实际花费(0.85x+30)元,若在乙商场购物,则实际花费(0.9x+10)元.(均用含x的式子表示);
(3)在(2)的情况下,请根据两家商场的优惠活动方案,讨论顾客到哪家商场购物花费少?说明理由.
分析 (1)计算出买160元的东西分别在甲、乙两商场的花费,然后得出在乙商场更少;
(2)根据甲、乙的优惠政策进行解答;
(3)根据(2)中表示出在甲乙两商场的花费列出的不等式,分情况讨论,求出最合适的消费方案.
解答 解:(1)在甲商店购买160元的东西需要花费:160(元),
在乙商场购买160元的东西需要花费:100+60×0.90=154(元),
∵160>154,
∴建议小明妈妈去乙商场花费少;
故答案是:乙;
(2)在甲商场购物:200+(x-200)×85%(或0.85x+30),
在乙商场购物:100+(x-100)×90%(或0.9x+10);
故答案是:(0.85x+30);(0.9x+10);
(3)①若在甲商场花费少,则0.85x+30<0.9x+10,
解得x>400
所以当购物超过400元时,到甲商场购物花费少;
②若在乙商场花费少,则0.85x+30>0.9x+10,
解得x<400,
所以当购物超过200元却少于400元时,到乙商场购物花费少;
③若到两家商场花费一样多时,则0.85x+30=0.9x+10
解得x=400
所以当购物400元时,到甲、乙两家商场购物花费一样.
点评 本题考查了一元一次不等式的应用,解答本题的关键是读懂题意,将现实生活中的事件与数学思想联系起来,列出不等式关系式即可求解.注意此题分类讨论的数学思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.在下列图形中,是轴对称图形而不是中心对称图形的是( )
| A. | 平行四边形 | B. | 等腰梯形 | C. | 菱形 | D. | 正六边形 |
10.能确定某学生在教室中的具体位置的是( )
| A. | 第3排 | B. | 第2排以后 | C. | 第2列 | D. | 第3排第2列 |
20.已知关于x的方程m2x2+(4m-1)x+4=0的两个实数根互为倒数,那么m的值为( )
| A. | 2 | B. | -2 | C. | ±2 | D. | ±$\sqrt{2}$ |
 从A地到B地有两条路,第一条从A地直接到B地,第二条从A地经过C,D到B地,两条路相比,第一条的长度=第二条的长度(填“<”“>”“=”)
从A地到B地有两条路,第一条从A地直接到B地,第二条从A地经过C,D到B地,两条路相比,第一条的长度=第二条的长度(填“<”“>”“=”)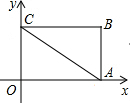 如图,已知矩形OABC的A点在x轴上,C点在y轴上,OC=6,OA=8.将△AOC沿AC对折,使点O落在点E处,AE交BC于N.
如图,已知矩形OABC的A点在x轴上,C点在y轴上,OC=6,OA=8.将△AOC沿AC对折,使点O落在点E处,AE交BC于N.