题目内容
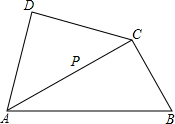 将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD的斜边恰好重合已知AB=2,P是AC上的一个动点.
将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD的斜边恰好重合已知AB=2,P是AC上的一个动点.(1)求AC的长;
(2)当点P在∠ABC的平分线上时,求DP的长;
(3)当点PD=BC时,求此时∠PDA的度.
考点:勾股定理,含30度角的直角三角形
专题:
分析:(1)根据∠CAB=30°,AB=2,利用三角函数的知识即可求解AC的长度;
(2)连接DP,作DH⊥AC,在Rt△BCP中,求出CP的长度,然后根据HP=HC-CP,求出HP的长度;
(3)当点PD=BC时,P点的位置可能有两处,分别为P1,P2,分别运用勾股定理求出PH的长度,然后求出∠HDP的度数,继而可求得∠PDA的度数.
(2)连接DP,作DH⊥AC,在Rt△BCP中,求出CP的长度,然后根据HP=HC-CP,求出HP的长度;
(3)当点PD=BC时,P点的位置可能有两处,分别为P1,P2,分别运用勾股定理求出PH的长度,然后求出∠HDP的度数,继而可求得∠PDA的度数.
解答:解:(1)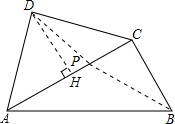 在Rt△ABC中,
在Rt△ABC中,
∵AB=2,∠CAB=30°,
∴BC=1,AC=
;
(2)连接DP,作DH⊥AC,
∵BP是∠ABC的角平分线,
∴∠CBP=30°,CP=
.
在Rt△ADC中,DH=AH=HC=
AC=
,
∴HP=
-
=
,
DP=
=
=
;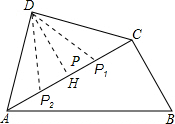
(2)当PD=BC=1时,P点的位置可能有两处,分别为P1,P2,
在Rt△DHP1中,HP1=
=
,
∴∠HDP1=30°,∠P1DA=30°+45°=75°,
同理,∠P2DA=45°-30°=15°.
∴∠PDA的度数为15°或75°.
 在Rt△ABC中,
在Rt△ABC中,∵AB=2,∠CAB=30°,
∴BC=1,AC=
| 3 |
(2)连接DP,作DH⊥AC,
∵BP是∠ABC的角平分线,
∴∠CBP=30°,CP=
| ||
| 3 |
在Rt△ADC中,DH=AH=HC=
| 1 |
| 2 |
| ||
| 2 |
∴HP=
| ||
| 2 |
| ||
| 3 |
| ||
| 6 |
DP=
| DH2+HP2 |
(
|
| ||
| 6 |

(2)当PD=BC=1时,P点的位置可能有两处,分别为P1,P2,
在Rt△DHP1中,HP1=
12-(
|
| 1 |
| 2 |
∴∠HDP1=30°,∠P1DA=30°+45°=75°,
同理,∠P2DA=45°-30°=15°.
∴∠PDA的度数为15°或75°.
点评:本题考查了勾股定理以及解直角三角形的应用,综合性较强,要熟练掌握好边角之间的关系以及勾股定理的应用,难度较大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
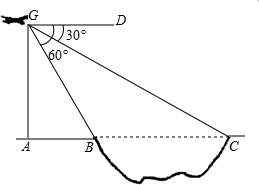 如图,为测得某一湖泊的宽度,在A处的正上方G处有一架飞行的飞机,此时正好测得湖泊东岸的点C处的俯角为30°,湖泊西岸的点B处的俯角为60°,此时飞机离地面的高度为900米,则湖泊的宽度是多少米?
如图,为测得某一湖泊的宽度,在A处的正上方G处有一架飞行的飞机,此时正好测得湖泊东岸的点C处的俯角为30°,湖泊西岸的点B处的俯角为60°,此时飞机离地面的高度为900米,则湖泊的宽度是多少米?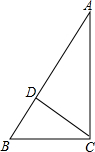 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,BC=3,AC=4,求AB、CD的长.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,BC=3,AC=4,求AB、CD的长.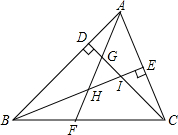 已知△ABC中,∠ABC=45°,且CD⊥AB于点D,BE⊥AC于点E,BE与CD交于点I.在BC上存在一点F,连接AF,使得∠BAF=∠ACD.AF交CD于点G,交BE于点H.
已知△ABC中,∠ABC=45°,且CD⊥AB于点D,BE⊥AC于点E,BE与CD交于点I.在BC上存在一点F,连接AF,使得∠BAF=∠ACD.AF交CD于点G,交BE于点H.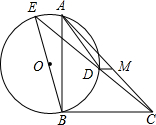 如图,BE是⊙O的直径,∠BAD=∠BCD,AB=5,BC=6,M为AC的中点.则DM=
如图,BE是⊙O的直径,∠BAD=∠BCD,AB=5,BC=6,M为AC的中点.则DM=