题目内容
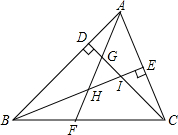 已知△ABC中,∠ABC=45°,且CD⊥AB于点D,BE⊥AC于点E,BE与CD交于点I.在BC上存在一点F,连接AF,使得∠BAF=∠ACD.AF交CD于点G,交BE于点H.
已知△ABC中,∠ABC=45°,且CD⊥AB于点D,BE⊥AC于点E,BE与CD交于点I.在BC上存在一点F,连接AF,使得∠BAF=∠ACD.AF交CD于点G,交BE于点H.(1)求证:AF=AC;
(2)试探究线段HI与FG的大小关系.
考点:全等三角形的判定与性质
专题:计算题
分析:(1)△ABC中,∠ABC=45°,且CD⊥AB,得到此三角形为等腰直角三角形,得到∠DBC=∠DCB=45°,由∠AFC为三角形ABF的外角,利用外角性质得到∠AFC=∠BAF+∠ABF,又因为∠ACF=∠ACD+∠DCB,根据∠BAF=∠ACD及等量代换得到∠ACB=∠AFC,利用等角对等边即可得证;
(2)FG=2HI,理由为:过F作FM垂直于AB,由一对直角相等,已知角相等且AF=AC,利用AAS得到三角形AFM与三角形ACD全等,利用全等三角形对应边相等得到AM=DC,再由三角形BDC为等腰直角三角形,得到BD=CD,等量代换得到AM=BD,根据同角的余角相等得到一对角相等,利用等角对等边得到AH=BH,再由一对直角相等,利用ASA得到三角形AFM与三角形BDI全等,利用全等三角形对应边相等得到AF=BI,根据AF-AH=BI-BH,得到HF=HI,利用等角的余角相等得到∠HGI=∠HIG,利用等角等边得到GH=HI,等量代换即可得证.
(2)FG=2HI,理由为:过F作FM垂直于AB,由一对直角相等,已知角相等且AF=AC,利用AAS得到三角形AFM与三角形ACD全等,利用全等三角形对应边相等得到AM=DC,再由三角形BDC为等腰直角三角形,得到BD=CD,等量代换得到AM=BD,根据同角的余角相等得到一对角相等,利用等角对等边得到AH=BH,再由一对直角相等,利用ASA得到三角形AFM与三角形BDI全等,利用全等三角形对应边相等得到AF=BI,根据AF-AH=BI-BH,得到HF=HI,利用等角的余角相等得到∠HGI=∠HIG,利用等角等边得到GH=HI,等量代换即可得证.
解答: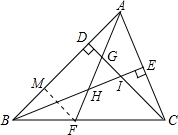 解:(1)∵△ABC中,∠ABC=45°,且CD⊥AB,
解:(1)∵△ABC中,∠ABC=45°,且CD⊥AB,
∴∠DBC=∠DCB=45°,
∵∠AFC为△ABF的外角,
∴∠AFC=∠DBC+∠BAF,
∵∠ACF=∠ACD+∠DCB,
∵∠BAF=∠ACD,∠DBC=∠DCB,
∴∠ACF=∠BAF,
∴AF=AC;
(2)FG=2HI,理由为:
过F作FM⊥AB,
在△AMF和△CDA中,
,
∴△AMF≌△CDA(AAS),
∴AM=CD,
∵△DBC为等腰直角三角形,
∴DB=DC,
∴AM=BD,
∵∠ABE+∠BAE=90°,∠ACD+∠CAD=90°,
∴∠ABE=∠ACD,
∵∠ACD=∠BAF,
∴∠ABE=∠BAF,
∴AH=BH,
在△AFM和△BID中,
,
∴△AFM≌△BID(ASA),
∴AF=BI,
∴AF-AH=BI-BH,即HF=HI,
∵∠AGD+∠GAD=90°,∠HGI=∠AGD,
∴∠HGI+∠GAD=90°,
∵∠ACD+∠CIE=90°,∠CIE=∠HIG,
∴∠HIG+∠ACD=90°,
∵∠GAD=∠ACD,
∴∠HGI=∠HIG,
∴HG=HI,
∴HG=HI=HF,
则FG=2HI.
 解:(1)∵△ABC中,∠ABC=45°,且CD⊥AB,
解:(1)∵△ABC中,∠ABC=45°,且CD⊥AB,∴∠DBC=∠DCB=45°,
∵∠AFC为△ABF的外角,
∴∠AFC=∠DBC+∠BAF,
∵∠ACF=∠ACD+∠DCB,
∵∠BAF=∠ACD,∠DBC=∠DCB,
∴∠ACF=∠BAF,
∴AF=AC;
(2)FG=2HI,理由为:
过F作FM⊥AB,
在△AMF和△CDA中,
|
∴△AMF≌△CDA(AAS),
∴AM=CD,
∵△DBC为等腰直角三角形,
∴DB=DC,
∴AM=BD,
∵∠ABE+∠BAE=90°,∠ACD+∠CAD=90°,
∴∠ABE=∠ACD,
∵∠ACD=∠BAF,
∴∠ABE=∠BAF,
∴AH=BH,
在△AFM和△BID中,
|
∴△AFM≌△BID(ASA),
∴AF=BI,
∴AF-AH=BI-BH,即HF=HI,
∵∠AGD+∠GAD=90°,∠HGI=∠AGD,
∴∠HGI+∠GAD=90°,
∵∠ACD+∠CIE=90°,∠CIE=∠HIG,
∴∠HIG+∠ACD=90°,
∵∠GAD=∠ACD,
∴∠HGI=∠HIG,
∴HG=HI,
∴HG=HI=HF,
则FG=2HI.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
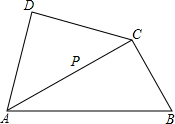 将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD的斜边恰好重合已知AB=2,P是AC上的一个动点.
将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD的斜边恰好重合已知AB=2,P是AC上的一个动点.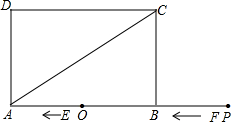 如图,矩形ABCD中,AB=6,BC=2
如图,矩形ABCD中,AB=6,BC=2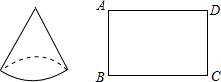 某工厂生产一批漏斗,工人师傅要把一块矩形铁皮加工成底面半径为20cm,高为40
某工厂生产一批漏斗,工人师傅要把一块矩形铁皮加工成底面半径为20cm,高为40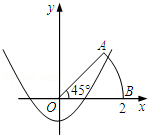 如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y=4x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是
如图,以扇形OAB的顶点O为原点,半径OB所在的直线为x轴,建立平面直角坐标系,点B的坐标为(2,0),若抛物线y=4x2+k与扇形OAB的边界总有两个公共点,则实数k的取值范围是