题目内容
2.已知关于x的函数y=(m+3)x|m|-3+2n-6是正比例函数,则mn=±12.分析 依据正比例函数的定义得到2n-6=0,|m|-3=1,然后可求得m、n的值,最后依据有理数的乘法法则进行求解即可.
解答 解:∵关于x的函数y=(m+3)x|m|-3+2n-6是正比例函数,
∴$\left\{\begin{array}{l}{2n-6=0}\\{|m|-3=1}\end{array}\right.$,解得n=3,m=±4.
∴mn=±12.
故答案为:±12.
点评 本题主要考查的是正比例函数的定义,依据正比例函数的定义列出方程组是解题的关键.

练习册系列答案
相关题目
13.用代数式表示比y的2倍少1的数,正确的是( )
| A. | 2( y-1 ) | B. | 2y+1 | C. | 2y-1 | D. | 1-2y |
 如图,在平面直角坐标系xOy中,已知A(-2,0),B(0,2),C是直线AB上的一个动点(不与点A,B重合),过点C作AB的垂线,交x轴于点D.
如图,在平面直角坐标系xOy中,已知A(-2,0),B(0,2),C是直线AB上的一个动点(不与点A,B重合),过点C作AB的垂线,交x轴于点D.

 如图,一架10米长的梯子AB,斜靠在一竖直的墙AC上,梯子的顶端距地面的垂直距离为8米,如果梯子的顶端沿墙下滑1米.
如图,一架10米长的梯子AB,斜靠在一竖直的墙AC上,梯子的顶端距地面的垂直距离为8米,如果梯子的顶端沿墙下滑1米.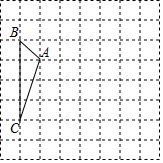 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上.
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上.