题目内容
已知等腰梯形ABCD中，AD∥BC，∠B=60°，BC-AD=3cm，则AB= ．
考点：等腰梯形的性质
专题：
分析：过点D作DE∥AB，交BC于点E，构建平行四边形ABED和等边△DEC．所以结合已知条件、平行四边形的性质以及等边三角形的性质来求AB边的长度．
解答：
解：如图，过点D作DE∥AB，交BC于点E，
∵AD∥BC，
∴四边形ABED是平行四边形，
∴AD=BE，AB=DE．
∵BC-AD=3cm，
∴EC=3cm．
∵在等腰梯形ABCD中，∠B=60°，
∴∠C=∠B=60°，
∴△DCE是等边三角形，
∴CE=DE=DC=3cm，
∴AB=DE=3cm．
故答案是：3cm．
解：如图，过点D作DE∥AB，交BC于点E，∵AD∥BC，
∴四边形ABED是平行四边形，
∴AD=BE，AB=DE．
∵BC-AD=3cm，
∴EC=3cm．
∵在等腰梯形ABCD中，∠B=60°，
∴∠C=∠B=60°，
∴△DCE是等边三角形，
∴CE=DE=DC=3cm，
∴AB=DE=3cm．
故答案是：3cm．
点评：本题考查了等腰梯形的性质，解题的关键是正确作出辅助线，把问题转化到平行四边形、等边三角形中来解决．
练习册系列答案
名校课堂系列答案
相关题目
如图，∠AOC=80°时，若三角板MON以每秒旋转5°的速度绕O点顺时针旋转一周，问多长时间后∠MOC=∠MOB？
如图，四边形ABCD中，AB=AD，BC=CD，AC，BD相交于E，由这些条件你能推出哪些结论（不再添加辅助线，不再标注字母，不写推理过程，只要求写出四个你认为正确的结论）？下列多项式中是二次二项式的是（ ）
| A、3x2+2x+1 |
| B、-x4+9 |
| C、x2-2x |
| D、x3-3x2+4 |
在正方形ABCD中，E是AD的中点，点F在DC上，且DF：FC=1：3，试判断△BEF的形状，并说明理由．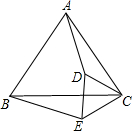
如图所示，已知：△ABC和△CDE都是等边三角形，求证：AD=BE．