题目内容
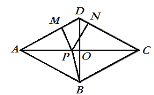
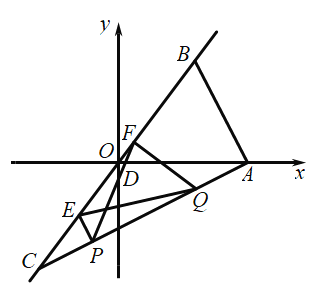
【题目】如图,在平面直角坐标系中,![]() 的斜边
的斜边![]() 在直线
在直线![]() 上,且
上,且![]() 是
是![]() 的中点,点
的中点,点![]() 的坐标为
的坐标为![]() .点
.点![]() 在线段
在线段![]() 上从
上从![]() 点向
点向![]() 点运动,同时点
点运动,同时点![]() 在线段
在线段![]() 上从
上从![]() 点向
点向![]() 点运动,且
点运动,且![]() .
.
(1)求![]() 的长及点
的长及点![]() 的坐标.
的坐标.
(2)作![]() 交
交![]() 于点
于点![]() ,作
,作![]() 交
交![]() 于点
于点![]() ,连结
,连结![]() ,
,![]() ,设
,设![]() .
.
①在![]() ,
,![]() 相遇前,用含
相遇前,用含![]() 的代数式表示
的代数式表示![]() 的长.
的长.
②当![]() 为何值时,
为何值时,![]() 与坐标轴垂直.
与坐标轴垂直.
(3)若![]() 交
交![]() 轴于点
轴于点![]() ,除点
,除点![]() 与点
与点![]() 重合外,
重合外,![]() 的值是否为定值,若是,请直接写出
的值是否为定值,若是,请直接写出![]() 的值,若不是,请直接写出它的取值范围.
的值,若不是,请直接写出它的取值范围.
【答案】(1)BC=10,B(3,4);(2)①![]() ;②
;②![]() 和
和![]() ;(3)为定值;
;(3)为定值;![]()
【解析】
(1)根据直角三角形斜边上的中线等于斜边的一半,设点B的坐标为![]() ,再利用勾股定理进行求解即可;
,再利用勾股定理进行求解即可;
(2)①由勾股定理求出AB,AC的长,进而求出![]() 的值,再利用三角函数求解CE,CF的长即可得出EF的长;
的值,再利用三角函数求解CE,CF的长即可得出EF的长;
②分两种情况讨论,当![]() 与
与![]() 轴垂直、
轴垂直、![]() 与x轴垂直,根据相似三角形的性质进行求解即可;
与x轴垂直,根据相似三角形的性质进行求解即可;
(3)作辅助线如图所示,根据![]() ,利用三角函数分别表示出CR和PI,进而表示出FN和PM即可求出
,利用三角函数分别表示出CR和PI,进而表示出FN和PM即可求出![]() .
.
(1)作![]() ,如图,
,如图,
设![]() 点坐标为
点坐标为![]() ,
,
∵点O是BC的中点,△ABC是直角三角形,
∴OA=OB=OC,
由勾股定理得:![]() ,
,
∴![]() ,
,
∴点![]() 的坐标为
的坐标为![]()
∴OB=5,
∴BC=10,
(2)①解:在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
由勾股定理得:![]() ,
,
∴![]() ,
,
∴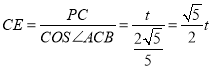 ,
,
![]() ,
,
∴![]() .
.
②1.当![]() 与
与![]() 轴垂直时,则
轴垂直时,则![]() ,如图,
,如图,
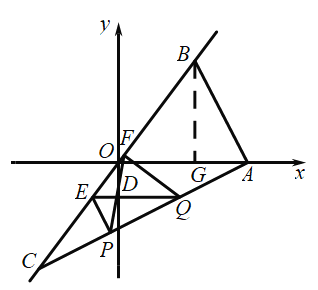
∴![]() ,
,
∴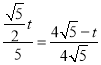 ,
,
∴![]() ,
,
∴![]() .
.
2.当![]() 与
与![]() 轴垂直时,则
轴垂直时,则![]() 轴,如图,
轴,如图,
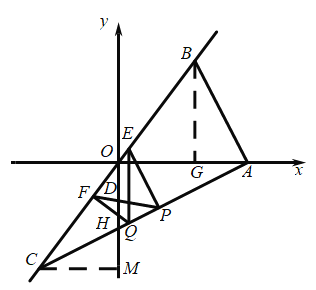
∴![]() ,作
,作![]() ,
,
∵![]() 点与
点与![]() 点关于
点关于![]() 点中心对称,
点中心对称,
∴![]() ,
,
∴![]() ,
,![]() ,
,
又![]() ,
,
∴
∴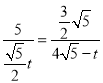 ,
,
∴![]() ,
,
∴![]()
综上所述:当![]() 和
和![]() 时,
时,![]() 与坐标轴垂直.
与坐标轴垂直.
(3)![]() 为定值.
为定值.
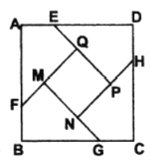
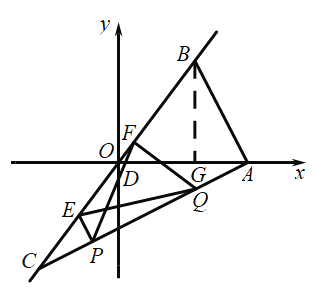
过点F作FR∥y轴,FN∥x轴,过点C作CK∥x轴,交FR于点R,CH∥y轴,过点P作MI∥x轴,如图所示,
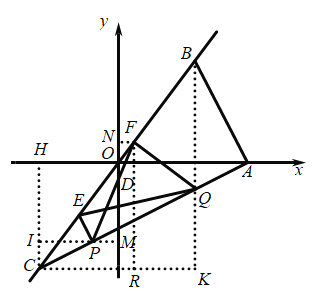
在Rt△BKC中,CK=6,BK=8,
∴![]() ,
,
在Rt△FRC中,
CR=![]() =
=![]() ,
,
∴FN=![]() ,
,
在Rt△CHA中,![]() ,
,
在Rt△CPI中,PI=![]() ,
,
∴![]() ,
,
∵PM∥FN,
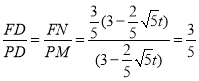 ,
,
故![]() 为定值.
为定值.

练习册系列答案
相关题目