Question

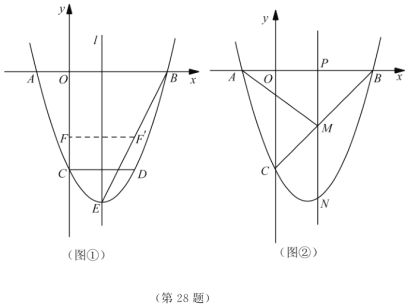
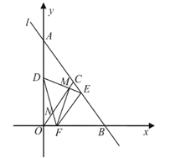
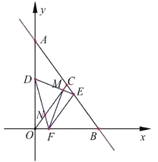
【题目】如图，在平面直角坐标系中，直线与轴、轴分别相交于、两点，点是的中点，点、分别为线段、上的动点，将沿折叠，使点的对称点恰好落在线段上（不与端点重合）.连接分别交、于点、，连接.

（1）求的值；

（2）试判断与的位置关系，并加以证明；

（3）若，求点的坐标.

Answer 1

【答案】（1）；（2），证明见解析；（3）点的坐标为.

【解析】

（1）结合A，B的坐标，在在中，即可求出的值；

（2）与的位置关系为，利用折叠的性质以及斜边上的中线定理可证明，再利用相似三角形的性质进一步证明，结合三角形内角和定理即可证明结论；

（3）设，则，，用含t的式子表示出DN，再由，得出OD的值，最后利用勾股定理求解即可．

解：（1）由题意得：，．

在中，．

（2），理由如下：

由折叠的性质得：．

∵为斜边上的中线，

∴，

∴，

∴．

又∵，

∴，

∴，即，

又∵，

∴，

∴，

∴，

∴，

∴．

（3）∵

∴在中，，

设，则，，

当时，．

又∵，，

∴，

∴，

∴．

由得：，即，

∴．

在中，由勾股定理得：，

即，解得：，，

∴或0（不合题意，舍去），

∴点．

综上所述，点的坐标为．