ƒøƒ⁄»ð
°æƒø°ø»ÁÕº£¨∂˛¥Œ∫Ø ˝![]() µƒÕºœÒ”Î
µƒÕºœÒ”Î![]() ÷·Ωª”⁄
÷·Ωª”⁄![]() °¢
°¢![]() ¡Ωµ„£¨”Î
¡Ωµ„£¨”Î![]() ÷·Ωª”⁄µ„
÷·Ωª”⁄µ„![]() £¨
£¨![]() £Æµ„
£Æµ„![]() ‘⁄∫Ø ˝ÕºœÒ…œ£¨
‘⁄∫Ø ˝ÕºœÒ…œ£¨![]() ÷·£¨«“
÷·£¨«“![]() £¨÷±œþ
£¨÷±œþ![]() «≈◊ŒÔœþµƒ∂‘≥∆÷·£¨
«≈◊ŒÔœþµƒ∂‘≥∆÷·£¨![]() «≈◊ŒÔœþµƒ∂•µ„£Æ
«≈◊ŒÔœþµƒ∂•µ„£Æ
£®1£©«Û![]() °¢
°¢![]() µƒ÷µ£ª
µƒ÷µ£ª
£®2£©»ÁÕº¢Ÿ£¨¡¨Ω”![]() £¨œþ∂Œ
£¨œþ∂Œ![]() …œµƒµ„
…œµƒµ„![]() πÿ”⁄÷±œþ
πÿ”⁄÷±œþ![]() µƒ∂‘≥∆µ„
µƒ∂‘≥∆µ„![]() «°∫√‘⁄œþ∂Œ
«°∫√‘⁄œþ∂Œ![]() …œ£¨«Ûµ„
…œ£¨«Ûµ„![]() µƒ◊¯±Í£ª
µƒ◊¯±Í£ª
£®3£©»ÁÕº¢⁄£¨∂ص„![]() ‘⁄œþ∂Œ
‘⁄œþ∂Œ![]() …œ£¨π˝µ„
…œ£¨π˝µ„![]() ◊˜
◊˜![]() ÷·µƒ¥πœþ∑÷±”Î
÷·µƒ¥πœþ∑÷±”Î![]() Ωª”⁄µ„
Ωª”⁄µ„![]() £¨”Î≈◊ŒÔœþΩª”⁄µ„
£¨”Î≈◊ŒÔœþΩª”⁄µ„![]() £Æ ‘Œ £∫≈◊ŒÔœþ…œ «∑ҥʑ⁄µ„
£Æ ‘Œ £∫≈◊ŒÔœþ…œ «∑ҥʑ⁄µ„![]() £¨ πµ√
£¨ πµ√![]() ”Î
”Î![]() µƒ√ʪ˝œýµ»£¨«“œþ∂Œ
µƒ√ʪ˝œýµ»£¨«“œþ∂Œ![]() µƒ≥§∂»◊Ó–°£ø»Áπ˚¥Ê‘⁄£¨«Û≥ˆµ„
µƒ≥§∂»◊Ó–°£ø»Áπ˚¥Ê‘⁄£¨«Û≥ˆµ„![]() µƒ◊¯±Í£ª»Áπ˚≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”…£Æ
µƒ◊¯±Í£ª»Áπ˚≤ª¥Ê‘⁄£¨Àµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®1£©![]() £¨
£¨![]() £ª£®2£©µ„
£ª£®2£©µ„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() £ª£®3£©µ„
£ª£®3£©µ„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() ∫Õ
∫Õ![]()
°æΩ‚Œˆ°ø
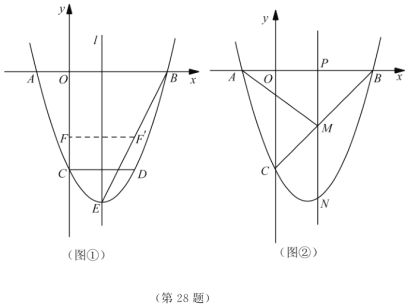
‘Â∑÷Œˆ£∫ £®1£©∏˘æð∂˛¥Œ∫Ø ˝µƒ∂‘≥∆÷·π´ Ω£¨≈◊ŒÔœþ…œµƒµ„¥˙»Î£¨º¥ø…£ª£®2£©œ»«ÛFµƒ∂‘≥∆µ„£¨¥˙»Î÷±œþBE£¨º¥ø…£ª£®3£©ππ‘Ï–¬µƒ∂˛¥Œ∫Ø ˝£¨¿˚”√∆‰–‘÷ «Ûº´÷µ.
‘Ã‚Ω‚Œˆ£∫.Ω‚£∫£®1£©![]() ÷·£¨
÷·£¨![]() £¨
£¨![]() ≈◊ŒÔœþ∂‘≥∆÷·Œ™÷±œþ
≈◊ŒÔœþ∂‘≥∆÷·Œ™÷±œþ![]()
![]()
![]() µ„µƒ◊¯±ÍŒ™
µ„µƒ◊¯±ÍŒ™![]()
![]() Ω‚µ√
Ω‚µ√![]() ªÚ
ªÚ![]() £®…·»•£©£¨
£®…·»•£©£¨![]()
£®2£©…˵„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]()
![]() ∂‘≥∆÷·Œ™÷±œþ
∂‘≥∆÷·Œ™÷±œþ![]() µ„
µ„![]() πÿ”⁄÷±œþ
πÿ”⁄÷±œþ![]() µƒ∂‘≥∆µ„
µƒ∂‘≥∆µ„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() .
.
![]() ÷±œþ
÷±œþ![]() æ≠π˝µ„
æ≠π˝µ„![]() ¿˚”√¥˝∂®œµ ˝∑®ø…µ√÷±œþ
¿˚”√¥˝∂®œµ ˝∑®ø…µ√÷±œþ![]() µƒ±Ì¥Ô ΩŒ™
µƒ±Ì¥Ô ΩŒ™![]() .
.
“ÚŒ™µ„![]() ‘⁄
‘⁄![]() …œ£¨
…œ£¨![]()
![]() º¥µ„
º¥µ„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]()
£®3£©¥Ê‘⁄µ„![]() ¬˙◊„“‚.…˵„
¬˙◊„“‚.…˵„![]() ◊¯±ÍŒ™
◊¯±ÍŒ™![]() £¨‘Ú
£¨‘Ú![]()
◊˜![]() ¥π◊„Œ™
¥π◊„Œ™![]()
![]()
![]()
¢Ÿµ„![]() ‘⁄÷±œþ
‘⁄÷±œþ![]() µƒ◊Û≤ý ±£¨
µƒ◊Û≤ý ±£¨![]() µ„µƒ◊¯±ÍŒ™
µ„µƒ◊¯±ÍŒ™![]() µ„µƒ◊¯±ÍŒ™
µ„µƒ◊¯±ÍŒ™![]() µ„µƒ◊¯±ÍŒ™
µ„µƒ◊¯±ÍŒ™![]()
![]() ‘⁄
‘⁄![]() ÷–£¨
÷–£¨![]() ±£¨
±£¨![]() »°◊Ó–°÷µ
»°◊Ó–°÷µ![]() .¥À ±
.¥À ±![]() µ„µƒ◊¯±ÍŒ™
µ„µƒ◊¯±ÍŒ™![]()
¢⁄µ„![]() ‘⁄÷±œþ
‘⁄÷±œþ![]() µƒ”“≤ý ±£¨
µƒ”“≤ý ±£¨![]() µ„µƒ◊¯±ÍŒ™
µ„µƒ◊¯±ÍŒ™![]() Õ¨¿Ì£¨
Õ¨¿Ì£¨![]() ±£¨
±£¨![]() »°◊Ó–°÷µ
»°◊Ó–°÷µ![]() .¥À ±
.¥À ±![]() µ„µƒ◊¯±ÍŒ™
µ„µƒ◊¯±ÍŒ™![]()
◊€…œÀ˘ ˆ£∫¬˙◊„“‚µ√µ„![]() µƒ◊¯±ÍŒ™
µƒ◊¯±ÍŒ™![]() ∫Õ
∫Õ![]()

 ÷¿≠ ÷»´”≈¡∑øºæÌœµ¡–¥∞∏
÷¿≠ ÷»´”≈¡∑øºæÌœµ¡–¥∞∏


