Question

如图，己知直线y=ax+b过A（-1，6）与y=

m

x

交于A点、B点，与y=

k

x

交于E点，直线y=ax+b与x轴交于C点，且AB=2BC=BE，则k=

10

．

Answer 1

分析：过A作AF⊥x轴，BG⊥x轴，如图所示，可得出△BCG∽△ACO，将A坐标代入第二象限的反比例解析式求出m的值，确定出反比例函数解析式，由AB=2BC，求出BC与AC之比，进而求出BG的长，即为B的纵坐标，代入反比例解析式求出B横坐标，确定出B坐标，将A与B坐标代入y=ax+b中求出a与b的值，确定出直线AB解析式，令y=0求出x的值，确定出C坐标，根据BE=2BC，得到C为BE中点，求出E坐标，代入第三象限反比例解析式中即可求出k的值．

解答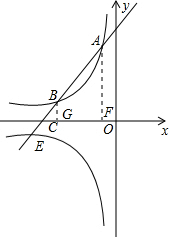：解：过A作AF⊥x轴，BG⊥x轴，如图所示，可得出△BCG∽△ACO，
将A坐标代入反比例y=

m

x

得：m=-6，即反比例解析式为y=-

6

x

，
∵A（-1，6），∴AF=6，OF=1，
∵AB=2BC=BE，
∴

BC

AC

=

BG

AF

=

1

3

，即BG=

1

3

AF=2，
将y=2代入y=-

6

x

得：x=-3，即B（-3，2），
将A与B坐标代入y=ax+b中得：

-3a+b=2 -a+b=6

，
解得：

a=2 b=8

，
∴直线AB解析式为y=2x+8，
令y=0，得到x=-4，即C（-4，0），
∵BE=2BC，即C为BE中点，
∴E（-5，-2），
将E坐标代入y=

k

x

中得：k=10．
故答案为：10．

点评：此题考查了反比例函数与一次函数的交点问题，涉及的知识有：相似三角形的判定与性质，线段中点坐标公式，待定系数法求函数解析式，熟练掌握待定系数法是解本题的关键．