题目内容
如果多项式P=a2+2b2+2a+4b+2015，则P的最小值是（ ）
| A、2011 | B、2012 |
| C、2013 | D、2014 |
考点：配方法的应用,非负数的性质：偶次方
专题：
分析：把p重新拆分组合，凑成完全平方式的形式，然后判断其最小值．
解答：解：p=a2+2b2+2a+4b+2015，
=（a2+2a+1）+（2b2+4b+2）+2012，
=（a+1）2+2（b+1）2+2012，
当（a+1）2=0，（b+1）2=0时，p有最小值，
最小值最小为2012．
故选B．
=（a2+2a+1）+（2b2+4b+2）+2012，
=（a+1）2+2（b+1）2+2012，
当（a+1）2=0，（b+1）2=0时，p有最小值，
最小值最小为2012．
故选B．
点评：此题主要考查了完全平方式的非负性，即完全平方式的值是大于等于0的，它的最小值为0，所以在求一个多项式的最小值时常常用凑完全平方式的方法进行求值．
练习册系列答案
相关题目
如图，AB是⊙O的直径，动弦CD垂直AB于点E，过点B作直线BF∥CD交AD的延长线于点F，若AB=10cm．
如图所示，∠α，∠β分别是四边形ABCD的外角，求证：∠α+∠β=∠A+∠C．下列说法正确的是（ ）
| A、有理数的绝对值都是正数 |
| B、0是单项式 |
| C、代数式分为单项式和多项式 |
| D、最小的整数是0 |
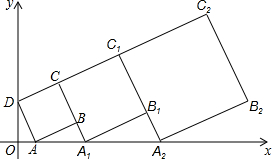在平面坐标系xOy中，正方形ABCD的位置如图所示，点A的坐标为（1，0），点D的坐标为（0，2），延长CB交x轴于点A1，作正方形A1B1C1C，延长C1B1交x轴于点A2，作正方形A2B2C2C1，求C2坐标．点A（x1，y1）和B（x2，y2）都在直线y=-
x-1上，且x1＞x2，则y1与y2的关系是（ ）
| 1 |
| 2 |
| A、y1≤y2 |
| B、y1=y2 |
| C、y1＜y2 |
| D、y1＞y2 |