题目内容
 如图,若∠EBC与∠BCF的平分线交于点G,试探究∠G与∠O的数量关系,并予以证明.
如图,若∠EBC与∠BCF的平分线交于点G,试探究∠G与∠O的数量关系,并予以证明.考点:三角形内角和定理,三角形的外角性质
专题:
分析:根据角平分线的性质可以求得∠GBC+∠GCB的值,即可求得∠G的值,再根据三角形内角和为180°可求得∠O的值,即可解题.
解答:解:∵∠EBC与∠BCF的平分线交于点G,
∴∠GBC=
∠EBC=
(180°-∠OBC),
∠GCB=
∠FCB=
(180°-∠OCB),
∴∠GBC+∠GCB=
(180°-∠OBC)+
(180°-∠OCB)=180°-
(∠OBC+∠OCB),
∴∠G=180°-(∠GBC+∠GCB)=
(∠OBC+∠OCB),
∴∠OBC+∠OCB=2∠G,
∵∠O=180°-(∠OBC+∠OCB),
∴∠O=180°-2∠G,即2∠G+∠O=180°.
∴∠GBC=
| 1 |
| 2 |
| 1 |
| 2 |
∠GCB=
| 1 |
| 2 |
| 1 |
| 2 |
∴∠GBC+∠GCB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴∠G=180°-(∠GBC+∠GCB)=
| 1 |
| 2 |
∴∠OBC+∠OCB=2∠G,
∵∠O=180°-(∠OBC+∠OCB),
∴∠O=180°-2∠G,即2∠G+∠O=180°.
点评:本题考查了角平分线平分角的性质,考查了三角形内角和为180°的性质,本题中求得∠G用∠OBC+∠OCB表示的值是解题的关键.

练习册系列答案
相关题目
以下列各组数为边长,能组成直角三角形的是( )
| A、8、15、7 |
| B、8、10、6 |
| C、5、8、10 |
| D、8、39、40 |
 等腰三角形ABC的腰长为10,底长为6.建立适当的直角坐标系,并写出各点的坐标.
等腰三角形ABC的腰长为10,底长为6.建立适当的直角坐标系,并写出各点的坐标.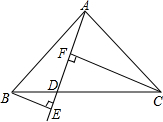 画一个两条直角边相等的直角三角形ABC,并过斜边BC上的一点D画射线AD,分别过B、C画射线AD的垂线BE、CF,垂足为E、F.
画一个两条直角边相等的直角三角形ABC,并过斜边BC上的一点D画射线AD,分别过B、C画射线AD的垂线BE、CF,垂足为E、F. 从图中能数出
从图中能数出