题目内容
5.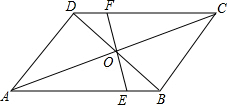 已知在?ABCD中,AC交BD于O,过O作直线交AB于E,交CD于F,若AB=8,AD=6,OF=2,求四边形BCFE的周长.
已知在?ABCD中,AC交BD于O,过O作直线交AB于E,交CD于F,若AB=8,AD=6,OF=2,求四边形BCFE的周长.
分析 由四边形ABCD是平行四边形,即可证得△AOE≌△COF,继而证得AE=CF,EF=2OF=2×2=4,继而求得四边形BCFE的周长.
解答 解:∵四边形ABCD是平行四边形,
∴AB∥CD,OA=OC,BC=AD=6,
∴∠OCF=∠OAE,
在△AOE和△COF,
$\left\{\begin{array}{l}{∠OAE=∠OCF}\\{OA=OC}\\{∠AOE=∠COF}\end{array}\right.$,
∴△AOE≌△COF(ASA),
∴AE=CF,EF=2OF=2×2=4,
∴四边形BCFE的周长为:EF+CF+BC+BE=EF+BC+AE+BE=EF+BC+AB=8+6+4=18.
点评 此题考查了平行四边形的性质以及全等三角形的判定与性质.注意证得△AOE与△COF全等是解此题的关键.

练习册系列答案
相关题目
 如图,按角的位置关系填空:∠1与∠2是同旁内角,∠1和∠3是同位角,∠2和∠4是对顶角,∠5与∠6是内错角.
如图,按角的位置关系填空:∠1与∠2是同旁内角,∠1和∠3是同位角,∠2和∠4是对顶角,∠5与∠6是内错角.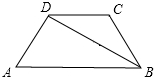 如图,在四边形ABCD中,DC∥AB,对角线BD平分∠ABC,且BD⊥AD,若AD=2,CD=3,则对角线BD的长为4$\sqrt{2}$.
如图,在四边形ABCD中,DC∥AB,对角线BD平分∠ABC,且BD⊥AD,若AD=2,CD=3,则对角线BD的长为4$\sqrt{2}$. 如图所示,圆O的半径为5,AB为弦,OC⊥AB,垂足为E,如果CE=2,那么AB的长是8.
如图所示,圆O的半径为5,AB为弦,OC⊥AB,垂足为E,如果CE=2,那么AB的长是8.