题目内容
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 切
切![]() 于点
于点![]() ,点
,点![]() 是
是![]() 上的一个动点(点
上的一个动点(点![]() 不与
不与![]() ,
,![]() 两点重合),连接
两点重合),连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
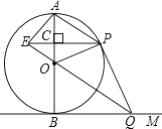
(1)求证:直线![]() 为
为![]() 的切线;
的切线;
(2)若直径![]() 的长为4.
的长为4.
①当![]() ________时,四边形
________时,四边形![]() 为正方形;
为正方形;
②当![]() ________时,四边形
________时,四边形![]() 为菱形.
为菱形.
【答案】(1)见解析;(2)①2;②![]() .
.
【解析】
(1)证![]() ,得出∠OPQ=∠OBQ=90°得证;
,得出∠OPQ=∠OBQ=90°得证;
(2)①根据四边形OBQP是正方形,可得点E与点O重合,故而求得EP的长;
②利用菱形的性质,对角线垂直且相互平分,可在Rt△CPO中求得CP的长,进而得出EP的长.
(1)证明:∵![]() 切
切![]() 于点
于点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() ,
,
而![]() ,
,
∴![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中
中
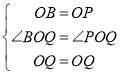 ,
,
∴![]() .
.
∴![]() .
.
∴直线![]() 为
为![]() 切线;
切线;
(2)①如下图所示
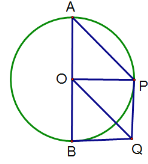
∵四边形OBQP是正方形
∴OP⊥AB
∴点O与点E重合
∴EP=OP
∵直径AB=4
∴OP=EP=2
②如下图
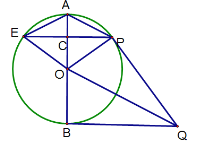
∵四边形AEOP是菱形
∴AO⊥EP,且AC=CO,EC=CP
∵直径AB=4
∴OP=2,CO=1
∴在Rt△PCO中,CP=![]()
∴EP=![]() .
.

练习册系列答案
相关题目