题目内容

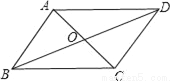
（1）如图，在□ABCD中，对角线AC、BD相交于点O．请找出图中的一对全等三角形，并给予证明；

（2）规定：一条弧所对的圆心角的度数作为这条弧的度数．

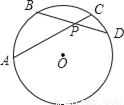
①如图，在⊙O中，弦AC、BD相交于点P，已知弧AB、弧CD分别为65°和45°，求∠APB；

②一般地，在⊙O中，弦AC、BD相交于点P，若弧AB、弧CD分别为m°和n°，求∠APB．

（用m、n的代数式表示）

（1）见解析；（2）①55°，②（m°+n°）． 【解析】【试题分析】 （1）答案不唯一，如：△AOB≌△COD．根据平行四边形的对角线相互平分，得AO=CO，OB=OD．因为对顶角相等，得∠AOB=∠COD，根据SAS，得：△AOB≌△COD． （2）①如图：连接AD， 根据弧AB、弧CD分别为65°和45°， 根据同弧所对的圆周角等于圆心角的一半，得∠ADB=65...
练习册系列答案
相关题目

有五张正面分别标有数字﹣2，﹣1，0，1，2的卡片，它们除数字不同外其余全部相同．现将它们背面朝上，洗匀后从中随机抽取一张，记卡片上的数字为a，则使关于x的一元二次方程x2﹣2（a﹣1）x+a（a﹣3）=0有两个不相等的实数根，且以x为自变量的二次函数y=x2﹣（a2+1）x﹣a+2的图象不经过点（1，0）的概率是__________．

【解析】试题分析：∵使关于x的一元二次方程x2-2（a-1）x+a（a-3）=0有两个不相等的实数根， ∴[-2（a-1）]2-4×1×a（a-3）＞0， 解得：a＞-1， ∵以x为自变量的二次函数y=x2-（a2+1）x-a+2的图象不经过点（1，0）， ∴12-（a2+1）-a+2≠0， ∴a≠1且a≠-2， ∴满足条件的a只有0和2， ∴使关于x的一...

如图所示，某数学活动小组选定测量小河对岸大树BC的高度，他们在斜坡上D处测得大树顶端B的仰角是30º，朝大树方向下坡走6米到达坡底A处，在A处测得大树顶端B的仰角是48°. 若坡角∠FAE=30°，求大树的高度. （结果保留整数，参考数据：sin48°≈0.74，cos48°≈0.67，tan48°≈1.11， ≈1.73）

13米． 【解析】试题分析：根据矩形性质得出DG=CH，CG=DH，再利用锐角三角函数的性质求出问题即可． 试题解析：如图，过点D作DG⊥BC于G，DH⊥CE于H， 则四边形DHCG为矩形． 故DG=CH，CG=DH， 在直角三角形AHD中， ∵∠DAH=30°，AD=6， ∴DH=3，AH=3， ∴CG=3， 设BC为x， 在直角三角形...

如图，在⊙O的内接四边形ABCD中，AB是直径，∠BCD=120°，过D点的切线PD与直线AB交于点P，则∠ADP的度数为（　　）

A. 40° B. 35° C. 30° D. 45°

C 【解析】试题分析：连接BD，∵∠DAB=180°﹣∠C=60°，∵AB是直径，∴∠ADB=90°，∴∠ABD=90°﹣∠DAB=30°，∵PD是切线，∴∠ADP=∠ABD=30°，故选C．

如图，已知矩形ABCD的边长AB=2，BC=3，点P是AD边上的一动点（P异于A、D），Q是BC边上的任意一点. 连AQ、DQ，过P作PE∥DQ交AQ于E，作PF∥AQ交DQ于F.

（1）求证：△APE∽△ADQ；

（2）设AP的长为x，试求△PEF的面积S△PEF关于x的函数关系式，并求当P在何处时，S△PEF取得最大值？最大值为多少？

（3）当Q在何处时，△ADQ的周长最小？（须给出确定Q在何处的过程或方法，不必给出证明）

（1）证∠APE=∠ADQ，∠AEP=∠AQD. 注意到△APE∽△ADQ与△PDE∽△ADQ，及S△PEF=， 得S△PEF==. ∴当，即P是AD的中点时，S△PEF取得最大值. （3）作A关于直线BC的对称点A′，连DA′交BC于Q，则这个点Q就是使△ADQ周长最小的点，此时Q是BC的中点. 【解析】（1）证得∠APE=∠ADQ，∠AEP=∠AQD，即可得到△APE∽...

一个口袋中有10个黑球和若干个白球若干个，从口袋中随机摸出一球，记下其颜色，再把它放回摇均，重复上述过程，共实验100次，其中25次摸到黑球，于是可以估计袋中共有白球_____个．

30 【解析】∵共实验100次，其中25次摸到黑球， ∴黑球所占的比例为=0.25，设袋中共有白球x个，则=0.25， 解得：x=30个． 故本题答案为：30．

如果圆锥的母线长为6cm，底面圆半径为3cm，则这个圆锥的侧面积为（　　）

A. 9πcm2 B. 18πcm2 C. 27πcm2 D. 36πcm2

B 【解析】底面圆半径为3cm，则底面周长=6π，圆锥的侧面积=×6π×6=18πcm2． 故选B．

关于x一元二次方程2x（kx-4）-x2+6=0没有实数根，则k的最小整数值是 。

2 【解析】试题分析：先把方程化为一般形式：（2k﹣1）x2﹣8x+6=0，由关于x的一元二次方程2x（kx﹣4）﹣x2+6=0没有实数根，所以2k﹣1≠0且△＜0，即解得k＞，即可得到k的最小整数值． 把方程化为一般形式：（2k﹣1）x2﹣8x+6=0， ∵原方程为一元二次方程且没有实数根， ∴2k﹣1≠0且△＜0，即△=（﹣8）2﹣4×（2k﹣1）×6=88﹣48k＜0...

某公司销售一种新型节能产品，现准备从国内和国外两种销售方案中选择一种进行销售．若只在国内销售，销售价格y（元/件）与月销量x（件）的函数关系式为y=x+150，成本为20元/件，无论销售多少，每月还需支出广告费62500元，设月利润为w内（元）．若只在国外销售，销售价格为150元/件，受各种不确定因素影响，成本为a元/件（a为常数，10≤a≤40），当月销量为x（件）时，每月还需缴纳x2元的附加费，设月利润为w外（元）．

（1）当x=1000时，y= 元/件，w内= 元；

（2）分别求出w内，w外与x间的函数关系式（不必写x的取值范围）；

（3）当x为何值时，在国内销售的月利润最大？若在国外销售月利润的最大值与在国内销售月利润的最大值相同，求a的值．

（1）140；57500；（2）w内= x2+130x﹣62500，w外=x2+（150﹣a）x．（3）30. 【解析】 试题分析：（1）将x=1000代入函数关系式求得y，并根据等量关系“利润=销售额﹣成本﹣广告费”求得w内； （2）根据等量关系“利润=销售额﹣成本﹣广告费”“利润=销售额﹣成本﹣附加费”列出两个函数关系式； （3）对w内函数的函数关系式求得最大值，再求出...

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网